SkriptPhysikZweiWellenMaschbau:Projekt Einsparzähler

Version [34014]

Dies ist eine alte Version von SkriptPhysikZweiWellenMaschbau erstellt von JulianOsthues am 2013-08-15 21:09:19.

HINWEIS
Das hier angebotene Skript kann und soll in keinen Fall den Gang zur Vorlesung ersetzen! Es dient lediglich zur Veranschaulichung; soll zu einigen Thematiken Tipps und Hilfestellungen geben und Ihnen helfen wichtige Zusammenhänge besser nachvollziehen zu können

\vec{E}

Vorlesungsskript Physik II

1. Wellen

1. Eindimensionale Wellen:

Defintion Welle: Eine Welle ist eine räumliche Ausbreitung eines Schwingungszustandes

Merke: Eine Welle ist eine räumliche und zeitliche Änderung einer physikalischen Größe

Es gibt zwei Möglichkeiten eindimensionaler Wellen sich auszubreiten:

- 1. Transversalwelle:

Hier verläuft die Schwingungsrichtung senkrecht zur Ausbreitungsrichtung (Abbildung 1a)

(z. B.: elektromagnetische Wellen, Wasserwellen oder auch Schallwellen in Festkörpern)

[Abbildung 1a; Quelle: http://www.weitensfelder.at/herbert/physik-tsunamis/laser_transversalwelle.gif]

- 2. Longitudinalwelle:

Hier verläuft die Schwingungsrichtung parallel zur Ausbreitungsrichtung (siehe Abbildung 1b)

(z. B.: Schallwellen in Gasen sowie in Flüssigkeiten, in manchen Fällen auch in Festkörpern)

[Abbildung 1b; Quelle: http://www.weitensfelder.at/herbert/physik-tsunamis/laser_longitudinalwelle.gif]

Die Amplitude u und die Wellenlänge λ:

Macht man eine Momentaufnahme einer Welle, zum Beispiel zum Zeitpunkt t = 0, lässt sich die Welle wie in der Abbildung 2 darstellen.
In dieser Aufnahme können wir nun die Amplitude und Wellenlänge λ sehr einfach einzeichnen und ablesen:

Die y-Achse stellt die Elongation (Auslenkung) zu einer bestimmten Zeit und Strecke dar und wird nachfolgend mit u bezeichnet.

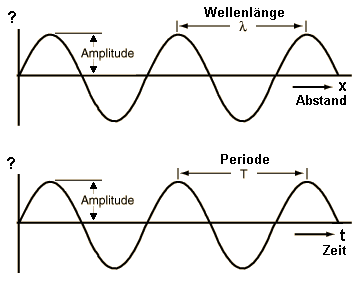
[Abbildung 2, Quelle: http://ivvgeo.uni-muenster.de/Vorlesung/GPS_Script/Bilder/Wellen/abb_4_1_2.gif]

Aus der bereits aus dem ersten Semester bekannten Formel Geschwindigkeit = Strecke/Zeit , also v = s/t können wir auf den Zusammenhang zwischen der Ausbreitungsgeschwindigkeit c, Wellenlänge λ und der Periode T schließen.

So ergibt sich für die Ausbreitungsgeschwindigkeit c:

c = λ / T bzw. c = λ* f

wobei die Frequenz f das Reziproke (Kehrwert) der Periode T, also f = 1/T ist.

1. Beispiel:
Berechnung einer Wellenlänge einer Schallwelle

Geg.: f = 435 s^-1, c = 340 m/s

λ = c/f

λ = 340 m*s/435 s

→ λ =0.78 m

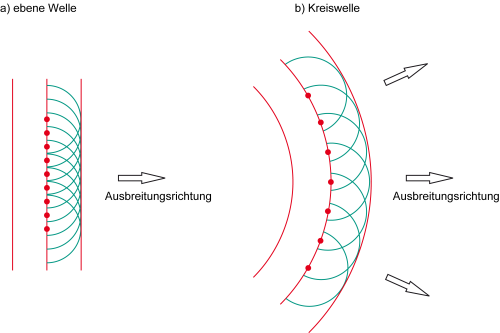
Wellenfront, Phase und das Huygensche Prinzip:

Auch in unserem Alltag sind wir praktisch zu jeder Zeit von Wellen umgeben; sei es das Licht, der Schall oder auch beispielsweise Mikrowellen. Diese breiten sich -wie bereits oben beschrieben- auf zwei Arten aus. Doch nicht nur das Verhältnis von Ausbreitungsrichtung zur Schwingungsrichtung bestimmt eine Welle.

Werfen wir beispielsweise einen Stein ins Wasser, so wissen wir, dass sich die Wellen kreisförmig um den "Einschlagort" ausbreiten werden.
Diese Form der Ausbreitung nennt man Kugelwellen (siehe Abbildung 2b).

Anders verhalten sich Wellen die z.B. durch eine Lautsprechermembran erzeugt werden.
Durch die in Schwingungen versetzte Membran entsehen hier ebene Wellen (siehe Abbildung 2a).

Sowohl kreisförmige, als auch ebene Wellen entstehen durch Interferenz (Überlagerung) sogenannter Elementarwellen. An bestimmten Stellen werden durch diese Überlagerung Wellenfronten ausgebildet.

Phase: Die Phase einer Welle gibt an, in welchem Abschnitt innerhalb einer Periode sich die Welle zu einem Referenzzeitpunkt und -ort befindet. Sie legt also fest, wie groß die Auslenkung ist.

Wellenfront: 3-Dimensionale Fläche, die alle Punkte gleicher Phase miteinander verbindet.

Nach dem Huygenschen Prinzipes bilden sich kreisförmige- und ebene Wellen wie folgt aus:

Huygenssche Prinzip: Nach diesem Prinzip kann jeder Punkt einer Wellenfront (also einer Fläche gleicher Phase) als Ausgangspunkt einer elementaren Kugelwelle (auch Elementarwelle genannt) aufgefasst werden.
Diese Sekundärwelle bewegt sich mit der gleichen Geschwindigkeit und hat die gleiche Frequenz und Phase wie die Primärwelle.

Die Einhüllende aller Elementarwellen ergibt die Wellenfront (der Primärwelle) zu einem späteren Zeitpunkt.

Der Abstand zwischen zwei "roten Linien" entspricht jeweils einer Wellenlänge λ

[Abbildung 3, Quelle: http://psi.physik.kit.edu/img/Ausbreitung.png]

1.1 Mathematische Beschreibung 1-dimensionaler Wellen:

Zur mathematischen Beschreibung von Wellen sind mehrere Größen nötig.
Dazu zählen unter anderem Amplitude, Phase, Ausbreitungs- oder Phasengeschwindigkeit und auch die Wellenzahl k.

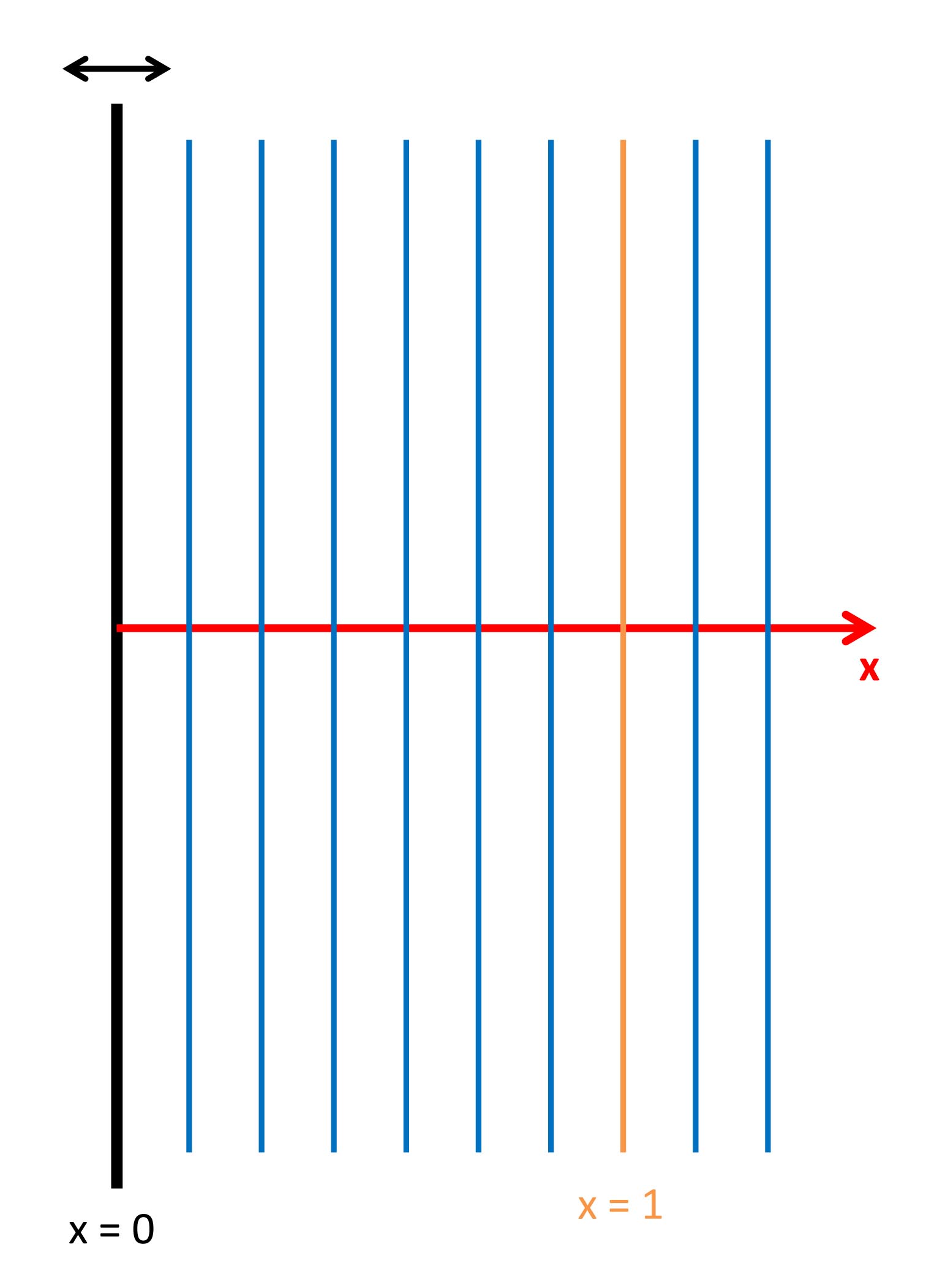
Die in Schwingung versetzte Membran erzeugt eine ebene Welle die sich entlang der x-Achse (roter Pfeil) nach rechts ausbreitet.

Die an x = 0 erzeugte Erregerschwingung: u (x=0, t) = u₀*sin (ω*t + φ₀), kommt am Ort x₁ mit einer Verzögerung von Δt an.

Daraus können wir für die Ausbreitungsgeschwindigkeit c folgern:
c = x/Δt, → Δt = x/c

→ u (x,t) = u₀*sin (ω*(t - Δt) + φ₀), mit Δt = x/c

⇒ u (x,t) = u₀*sin (ω*t - (ω*x / c) + φ₀)

[Abbildung 4]

Einführung der Wellenzahl k:

Wir definieren: die Wellenzahl k = 2 π / λ

→ λ = 2 π / k

mit ω = 2 π * f , (das wir umstellen zu f = ω / 2 π) und c = λ * f erhalten wir: c = (2π / k) * (ω / 2π)
→ c = ω / k

umgestellt ergibt sich also für die Wellenzahl k = ω / c.

daraus folgt für die allgemeine Wellengleichung in Abhängingkeit vom Ort x und der Zeit t:

Wichtig: ist die Wellenzah k in der Wellengleichung:

negativ, so verläuft die Welle nach →

positiv, so verläuft die Welle nach ←

u(x,t) = u₀*sin (ω*t - k*x + φ₀)

2. Beispiel:
Eine Wasserwelle wird durch die Funktion u(x,t) = 30mm * sin (2 π * (t / 0.3s) - (x / 0.1m) + π / 6) beschrieben.

Gesucht:
Bestimmen Sie die Ausbreitungsgeschwindigkeit c

Gegeben:
u(x,t) = 30mm * sin (2 π * (t / 0.3s) - (x / 0.1m) + π / 6) → u(x,t) = 30mm * sin (2 π* t / 0.3s) - (2 π* x / 0.1m) + π / 6)

Vergleichen wir diese mit der allgemeinen Wellengleichung u(x,t) = u₀*sin (ω*t - k*x + φ₀), sehen wir:

u₀ = 30mm

ω = 2π / T = 2π / 0.3s → T = 0.3s

k = 2π / λ = 2π / 0.1m → λ = 0.1m

φ = π / 6

Da die Ausbreitungsgeschwindigkeit c = λ / T ist,

⇒ c = 0.1m / 0.3s = 0.333m/s

Herleitung der Differentialgleichung einer 1-Dimensionalen Welle:

Wir wollen die Differentialgleichung einer eindimensionalen Welle herleiten und beginnen mit der allgemeinen Wellengleichung, die sich aus folgenden Komponenten zusammensetzt:

u₀ = Amplitude

ω = Kreisfrequenz

k = Wellenzahl

φ = Anfangsphase

→ u(x,t) = u₀*sin (ω*t - k*x + φ₀)

Nun leiten wir diese allgemeine Wellengleichung u(x,t) nach dem Ort x partiell ab, was mathematisch korrekt in dieser Weise dargestellt wird: ∂u/∂x.

Kleiner Ableitungshelfer:

Die Variable nach der abgeleitet wird ist in rot und
alle Werte die sich durch die jeweilige Ableitung geändert haben, sind in grün dargestellt

→ ∂u/∂x = u₀*cos (ω*t - k*x + φ₀) * (- k)

Die zweite Ableitung ∂²u/∂x² lautet dann:

∂²u/∂x² = u₀*- sin ((ω*t - k*x + φ₀) * (- k) * (- k)

→ ∂²u/∂x² = - k²*u₀ *sin (ω*t - k*x + φ₀)

Als nächstes leiten wir die allgemeine Wellengleichung u(x,t) nach der Zeit t partiell ab, also: ∂u/∂t.

→ ∂u/∂x = u₀*cos (ω*t - k*x + φ₀) * (ω)

Die zweite Ableitung ∂²u/∂t² lautet dann:

∂²u/∂t² = u₀*- sin (ω*t - k*x + φ₀) * (ω) * (ω)

→ ∂²u/∂t² = - ω² u₀*sin (ω*t - k*x + φ₀)

Als letzten Schritt verbinden wir die beiden partiellen Ableitungen ∂²u/∂x² und ∂²u/∂t² in dem wir sie:

1. Umstellen:

∂²u/∂x² = - k²*u₀ *sin (ω*t - k*x + φ₀) ⇒ ∂²u/∂x² = 1 / k²

∂²u/∂t² = - ω² u₀*sin (ω*t - k*x + φ₀) ⇒ ∂²u/∂t² = 1 / ω²

2. Gleichsetzen:

∂²u/∂x² = 1 / k² = ∂²u/∂t² = 1 / ω²

→ ∂²u/∂x² = (k² / ω²) * ∂²u/∂t²

mit k = ω/c erhalten wir:

∂²u/∂x² = (ω² / c²*ω²) * ∂²u/∂t²

⇒ Die differentielle 1-dimensionale Wellengleichung lautet daher: ∂²u/∂x² = ( 1 / c²) * ∂²u/∂t²

1.2 Interferenz

Konstruktive und Destruktive Interferenz:

Superposition bedeutet in der Wellenlehre die ungestörte Überlagerung (Interferenz) mehrerer Wellen des gleichen Typs.
Die relevante Größe der Überlagerung ist die Amplitude u (Höhe) der einzelnen Wellen. So können sich beispielsweise mehrere Wasserwellen oder mehrere elektromagnetische Wellen gegenseitig überlagern.

Von Interferenz spricht man, wenn zwei oder mehr Wellen aufeinenander treffen, sich durchdringen und interferieren, also sich überlagern (siehe Abbildung 4). Diese Überlagerung kann man durch das sogenannte Superpositionsprinzip beschreiben.

[Abbildung 5, "stehende Welle"; Quelle: http://upload.wikimedia.org/wikipedia/commons/3/3c/Standing_waves1.gif]

Beispiel 3: Anwendung des Superpositionsprinzipes:

Überlagerung von zwei 1-dimensionalen Wellen mit folgenden Eigenschaften:

gleiche Amplitude u

gleiche Frequenz f₁ = f₂

gleiche Wellenlänge und Wellenzahl, also ω₁ = ω₂ und k₁ = k₂

feste Phasenbeziehung Δφ = const.

⇒ Δ ω = 0, Δ k = 0

→ Dadurch entsteht eine neue Wellengleichung für diese beiden interferierenden Wellen: u(x,t) = 2*u₀*cos (Δφ/2)*sin (ω*t - k*x + φ)

Die effiktive Amplitude A_eff = 2*u₀*cos (Δφ/2) bewegt sich hier also im Bereich von 0....2u₀!

Anwendung der Superposition:

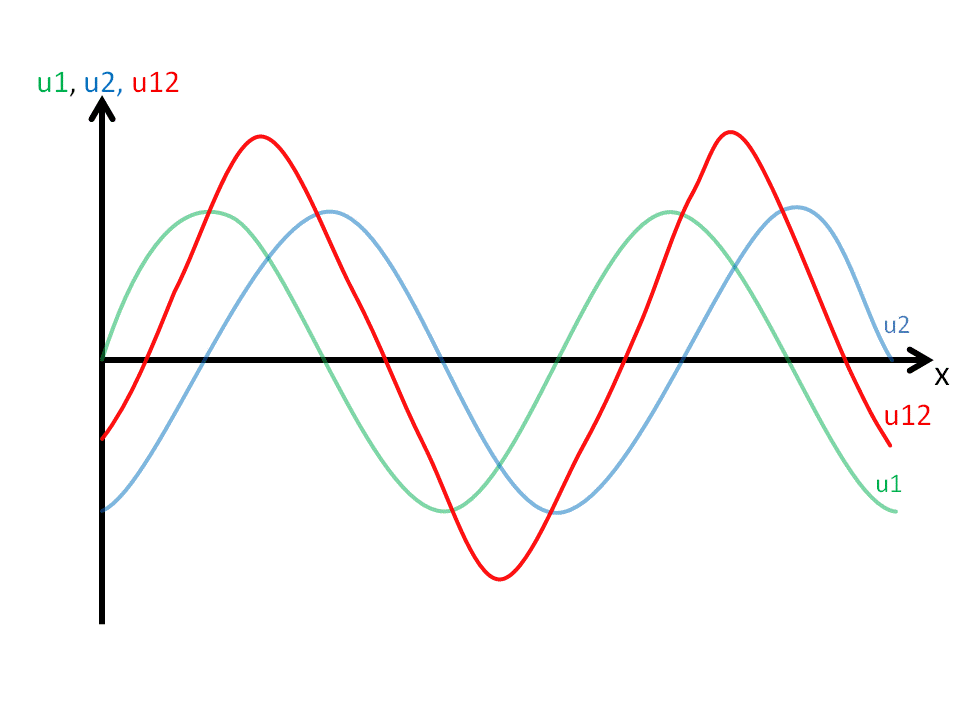
In der Abbildung 5 interferieren zwei eindimensionale Wellen u1 und u2 mit den links beschriebenen Eigenschaften.

Hierbei werden an verschiedenen beliebigen Punkten der x-Achse die beiden Amplituden der Wellen mit Vorzeichen addiert. Verbindet man diese Punkte miteinander entsteht dadurch eine neue Welle: in unserem Beispiel ist dies die Welle u12.

Diese Addition der Amplituden der einzelnen Wellen nennt man Superposition.

[Abbildung 6]

Bei der Überlagerung von Wellen können natürlich fast unendliche viele Möglichkeiten entstehen; nämlich je nachdem wie die Wellen aufeinander treffen, welche Frequenz sie haben ob die Phasendifferenz variiert usw.

Je nach Konstellation verhalten sich die beiden aufeinander treffenden Wellen, und die dadruch entstehende Welle, anders.
Dementsprechend können nun verschiedene Fälle je nach Wellenabschnitt eintreten:

Die Wellen können sich gegenseitig:

verstärken,

abschwächen

oder sogar auslöschen.

Dabei treten zwei bemerkenswerte Grenzfälle auf:

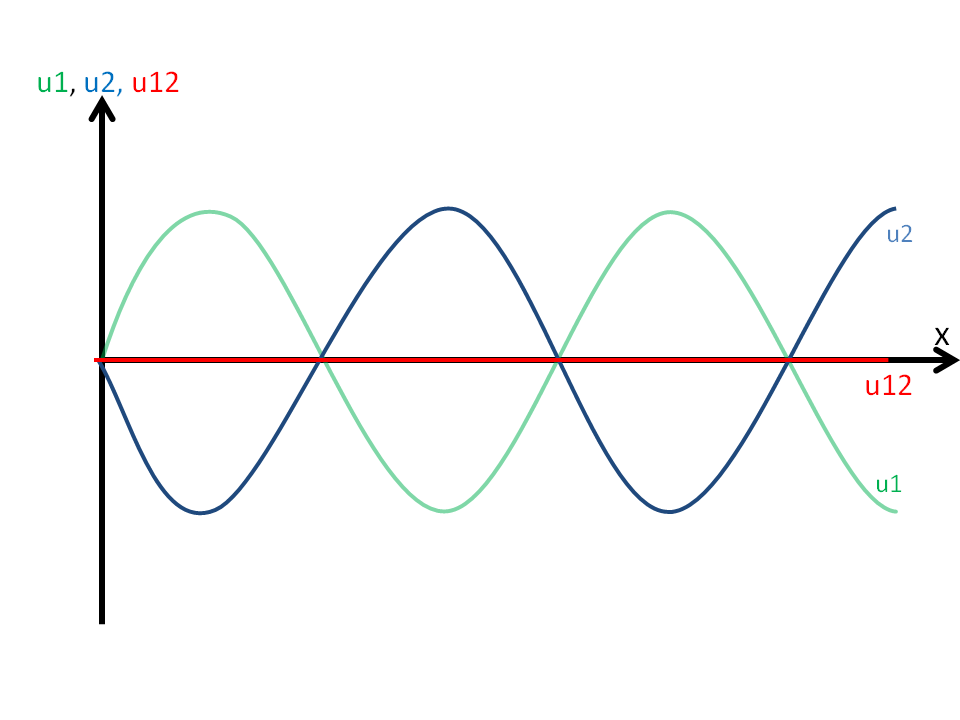
Grenzfall 1: Destruktive Interferenz (Auslöschung):

Damit eine destruktive Interferenz eintreten kann, muss die Effektive Amplitude der beiden Wellen A_eff = 0 sein (siehe Abbildung 7).

Wenn wir uns die allgemeine Wellengleichung für zwei interferierende Wellen, gleicher Amplitude, gleicher Frequenz und fester Phasenbeziehung ansehen

u(x,t) = 2*u₀*cos (Δφ/2)*sin (ω*t - k*x + φ) bedeutet das:

→ cos (Δφ/2) = 0 → Δφ/2 = (π/2)

⇒ für die Phasendifferenz Δ φ = π, und dementsprechend auch alle anderen ungeradzahligen Vielfachen von π: ±3π, ±5π, ±7π,...

Ist dies der Fall, entsteht durch die Wellen u1 und u2 folgende Welle u12:

[Abbildung 7]

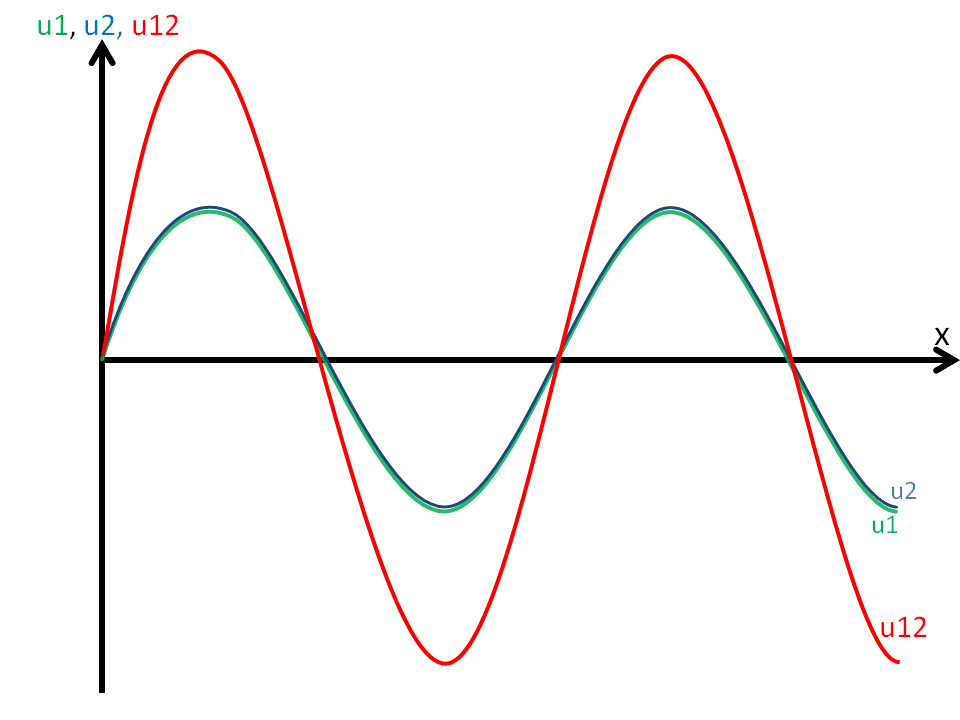
Grenzfall 2: Konstruktive Interferenz (Verstärkung):

Damit eine konstruktive Interferenz eintreten kann, muss die Effiktive Amplitude der beiden Wellen A_eff = 2u₀ sein (siehe Abbildung 8).

Auch hier betrachten wir die allgemeine Wellengleichung zwei interferierender Wellen, gleicher Amplitude, gleicher Frequenz und fester Phasenbeziehung und stellen fest,

dass aus A_eff = 2u₀ folgt:

→ cos (Δφ/2) = 1 → Δφ/2 = 0

⇒ für die Phasendifferenz Δ φ = 0 , und dementsprechend auch alle anderen geradzahligen Vielfachen von π: ±2π, ±4π, ±6π,...

Ist dies der Fall, entsteht durch die Wellen u1 und u2 folgende Welle u12:

[Abbildung 8]

2. Elektromagnetische Wellen

Elektromagnetische Wellen:

Eine elektromagnetische Welle ist eine Welle aus gekoppelten elektrischen und magnetischen Feldern.

Das alltägliche, vertrauteste Beispiel einer elektromagnetischen Welle ist sichtbares Licht. Ebenfalls eine natürliche, alltägliche Erscheinung elektromagnetischer Wellen ist die unsichtbare Wärmestrahlung, das so genannte »Infrarot«, sowie das ebenfalls unsichtbare Ultraviolett. Diese natürlich entstehenden Formen elektromagnetischer Wellen können für spezielle Zwecke auch künstlich erzeugt und technisch genutzt werden.

Elektromagnetische Wellen sind also:

Der schottische Physiker James Clerk Maxwell erarbeitete die nach ihm benannten Gleichungen von 1861 bis 1864. Er kombinierte dabei das Durchflutungsgesetz und das gaußsche Gesetz mit dem Induktionsgesetz.

Die Maxwell-Gleichungen sind ein spezielles System von linearen partiellen Differentialgleichungen erster Ordnung. Die Gleichungen beschreiben den Zusammenhang von elektrischen und magnetischen Feldern mit elektrischen Ladungen und elektrischem Strom unter gegebenen Randbedingungen.

→ Räumlich und zeitlich periodische Änderung des elektrischen Feldes