Tutorium Mathematik 3
Lambda - Ansatz
Differentialgleichungen
| 1.3 Lösen Sie die folgenden linearen homogenen Differentialgleichungen mit konstanten Koeffizienten mittels der charakteristischen Gleichung Aufgabe 1.3.1 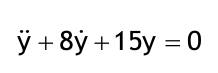 Aufgabe 1.3.2 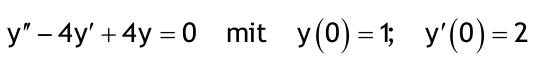 Aufgabe 1.3.3 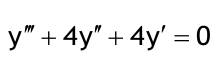 Aufgabe 1.3.4  Aufgabe 1.3.5 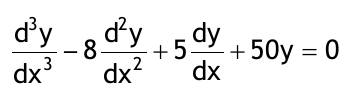 Aufgabe 1.3.6 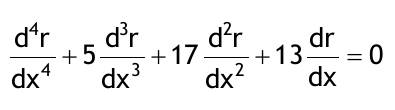 Aufgabe 1.3.7 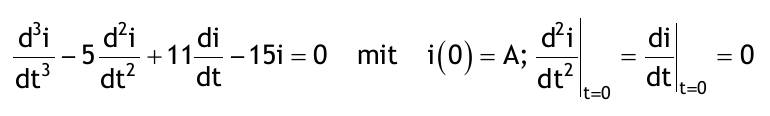 Aufgabe 1.3.8  |
| Aufgabe 1.3.1: y..+8y.+15y=0 Aufgabe 1.3.2: y(2 Strich)-4y'+4y=0 mit y(0)=1; y'(0)=2 Aufgabe 1.3.3: y(3 Strich)+4y(2 Strich)+4y'=0 Aufgabe 1.3.4: (d^2u)/(dt^2)+8du/dt+25u=0 mit u(0)=A; u.(0)=0 Aufgabe 1.3.5: (d^3y)/(dx^3)-8(d^2y)/(dx^2)+5dy/dx+50y=0 Aufgabe 1.3.6: (d^4r)/(dx^4)+5(d^2r)/(dx^3)+17(d^2r)/(dx^2)+13(dr/dx)=0 Aufgabe 1.3.7: (d^3i)/(dt^3)-5(d^2i)/(dt^2)+11(di/dt)-15i=0 mit i(0)=A; (d^2i)/(dt^2)=di/dt mit t=0=0 |
| PDF Dokument Lambda - Ansatz |

