Version [61353]
Dies ist eine alte Version von TutoriumE3A2 erstellt von Jorina Lossau am 2015-11-15 16:12:11.
Tutorium Elektrotechnik 3
| File | Last modified | Size |
|---|---|---|
| E3A2.pdf | 2023-10-06 18:37 | 99Kb |
| E3A21.jpg | 2023-10-06 18:37 | 86Kb |
| E3A22.jpg | 2023-10-06 18:37 | 87Kb |
| schaltung1.jpg | 2023-10-06 18:37 | 8Kb |
| schaltung10.jpg | 2023-10-06 18:37 | 9Kb |
| schaltung11.jpg | 2023-10-06 18:37 | 7Kb |
| schaltung2.jpg | 2023-10-06 18:37 | 5Kb |
| schaltung3.jpg | 2023-10-06 18:37 | 13Kb |
| schaltung4.jpg | 2023-10-06 18:37 | 8Kb |
| schaltung5.jpg | 2023-10-06 18:37 | 11Kb |
| schaltung6.jpg | 2023-10-06 18:37 | 4Kb |
| schaltung7.jpg | 2023-10-06 18:37 | 4Kb |
| schaltung8.jpg | 2023-10-06 18:37 | 8Kb |
| tutorium_get_3_teil_2.pdf | 2023-10-06 18:37 | 188Kb |
| tutorium_get_3_teil_3.pdf | 2023-10-06 18:37 | 114Kb |
Ströme, Spannungen und Widerstände in RLC-Schaltungen
| 1.1 Beispielaufgabe Gegeben ist folgende Schaltung mit einer trigonometrischen Wechselspannungsquelle.  Die Bauteile haben folgende Kenndaten: R = 100Ω L = 1H C = 30µF f = 50 Hz u = 325 V a) Geben Sie u(t) als komplexes, imaginäres und reelles Zeitsignal an b) Geben Sie den Blindwiderstand XL an. c) Geben Sie den Blindleitwert BC an. d) Ermitteln Sie die komplexen Amplituden der Ströme iL, iR und iges mit Hilfe der komplexen Wechselstromrechnung e) Ermitteln Sie die komplexen Amplituden der Spannungen uC und uLR, mit Hilfe der komplexen Wechselstromrechnung. f) Geben Sie die Zeigerbilder der errechneten Ströme und Spannungen an. g) Geben Sie die Zeitsignale der errechneten Ströme und Spannungen an. Lösung: a) u(t) = u*(cos(2πft)+j* sin(2πft)) u(t) = 325V*(cos(2π*50Hz*t)+j*sin(2π*50Hz*t)) Re(u(t)) = 325V*cos(2π*50Hz*t) Im(u(t)) = 325V*sin(2π*50Hz*t) b) XL = wL = 2π* 50 Hz* 1H = 2π*50s^-1*1VsA^-1= 100πV/A=314,16Ω c) BC = wC = 2π* 50Hz* 30µF = 2π*50s^ -1*30*10^ -6AsV^ -1 = 9,425*10^ -3S d) YLR =1/R + 1/jwL = (jwL + R)/jwRL --> ZLR = jwRL/(jwL+R) ZC = 1/jwC Zges = 1/jwC + jwRL/(jwL + R) Erweiterung des zweiten Terms mit dem konjugiert Komplexen. Zges = 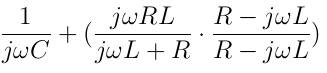 Zges = 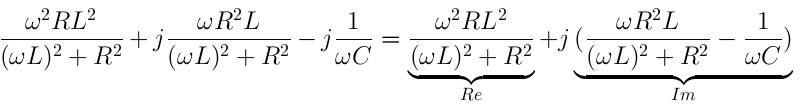 ReZges = 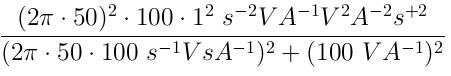 =90,8 Ω ImZges = 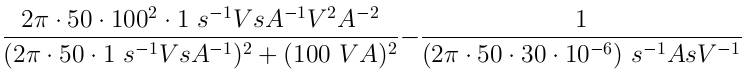 ImZges = -77,3Ω Z = √(Re² + Im²) = √(8244,64Ω² + 5959,84Ω² = 119,2Ω ℓ = arctan(Im/Re) = arctan(-77,2Ω/90,8Ω) =-40,37 Grad iges = u/Z = 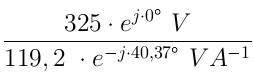 = 2,73* e^(j*40,37Grad) A Errechnung der restlichen Ströme mit Hilfe der Stromteilerregel. iR/iges = YR/YLR = (1/R)/((1/R)+(1/jwL)) = jwL/(R+jwL) = (j*314,16Ω)/((100+j*314,16)Ω) iR = jwL/(R+jwL)*iges = ((314,16*e^(j*90Grad)Ω)/((329,69*e^(j*72,34Grad)Ω)*2,73*e^j*40,37Grad A = 314,16Ω/329,69Ω*2,73A iR = (314,16Ω/329,69Ω)*2,73A*e^(j*(90Grad+40,37Grad-72,34Grad)) = 2,6*e^(j*58,03Grad)A iL = YL/YLR*iges = R/(R+jwL)*iges = (100*e^(j*0Grad)Ω)/((329,69*e^(j*72,43Grad)Ω))*2,73*e^(j*40,37Grad)A iL = 0,83*e^(-j*31,91Grad)A uC = ZC*iC = 106,1*e^(-j*90Grad)VA^ -1*2,73*e^(j*40,37Grad) A = 289,65*e^(-j*49,63Grad)V |
| PDF Dokument Teil 2 |

