Version [71957]
Dies ist eine alte Version von Mathe3TutoriumLambda erstellt von Jorina Lossau am 2016-09-26 14:12:00.
Tutorium Mathematik 3
Lambda - Ansatz
| Geeignet für lineare homogene DGL mit konstanten reellen Koeffizienten. Normalform: 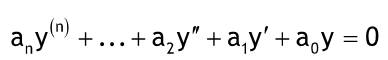 any^(n)y+...+a2y(2 Strich)+a1y'+a0y=0 Charakteristische Gleichung: 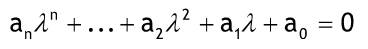 anλ^n+...+a2λ^2+a1λ+a0=0 Der Lambda-Ansatz liefert ein Polynom mit denselben Koeffizienten wie die DGL. Es hat n Lösungen, die einfach, mehrfach reell oder zumindest konjugiert komplex sein können.  einfache reelle Lösung λ->eine Teillösung y1=C1*exp(λx) k-fache reelle Lösung λ-> k Teillösung xj=Cj*e^(j-1)exp(λx); j=1,...,k 2 konjugiert komplexe Lösungen λ1,2=a+- jw -> y1,2=e^ax(A*cos(wx)+B*sin(wx) Die allgemeine Lösung der DGL ist die Summe aller Teillösungen. Beispiele:  |
| PDF Dokument Lambda - Ansatz |

