Tutorium Mathematik 3
Laplace - Transformation
Wichtige Rechenregeln und ausgewählte Korrespondenzen der Laplace – Transformation
| Originalbereich, Zeitbereich | Bildbereich | Originalfunktion, Zeitfunktion | Bildfunktion | |
|---|---|---|---|---|
| f(t), g(t) | F (s), G (s) | 1 | 1/s | |
| Linearitätsregel | 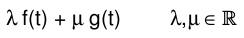 λt(t)+μg(t) wobei λ,μЄR | 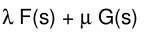 λF(s)+μG(s) | e^(αt) | 1/(s-α) |
| Differentationsregel (1.) | f.(t) | s F(s) - f(0) | t | 1/s² |
| Differentationsregel (2.) | f..(t) | s² F(s) - s f(0) | t² | 2/s³ |
| Differentationsregel (n-te) | f^ n(t) | 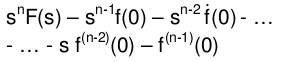 s^nF(s)-s^(n-1)f(0)-s^(n-2)j(0)-..-sf^(n-2)(0)-f^(n-1)(0) | t^ n | n!/s^(n+1) |
| Integrationsregel | 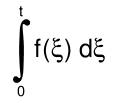 ∫f(ξ)dξ wobei ∫ von 0 bis 1 | 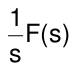 (1/s)F(s) | 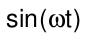 sin(ωt) | 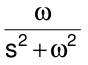 ω/(s^2+ω^2) |
| Dämpfungsregel | 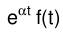 e^(αt)f(t) | 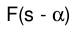 F(s-α) | 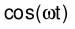 cos(ωt) | 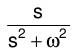 s/(s^2+ω^2) |
| Faltungsregel | 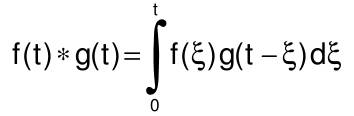 f(t)*g(t)*g(t)=∫f(ξ)g(t-ξ)dξ wobei ∫ von 0 bis t | F(s)* G(s) | 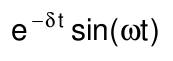 e^(-δt)sin(ωt) | 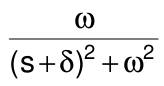 ω/((s+δ)^2+ω^2) |
| Verschiebungsregel (Versch. nach rechts) | f(t-a) | 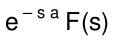 e^(-sα)F(s) | 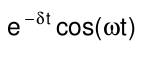 e^(δt)cos(ωt) | 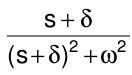 (s+δ)/((s+δ)^2+ω^2) |
| PDF Dokument Laplace - Transformation |

