Tutorium Mathematik 3
Laplace - Transformation - Lösungen
| Aufgabe 2.1 Nachfolgend für t ≥ 0 definierte Funktionen haben für t < 0 den Funktionswert f(t) = 0. Transformieren Sie mit der Tabelle in den Bildbereich der Laplace-Transformation! 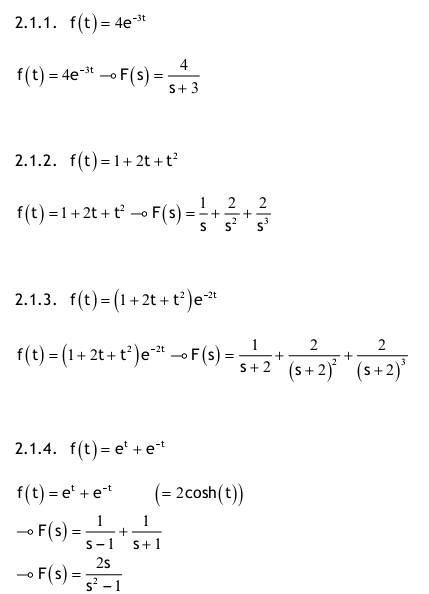 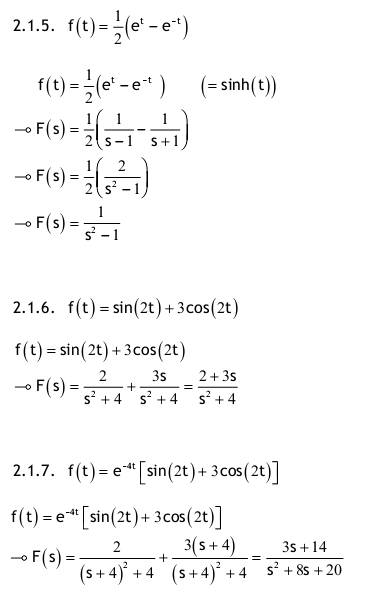 2.1.1. f(t)=4e^(-3t) ->F(s)=4/(s+3) 2.1.2. f(t)=1+2t+t^2 ->F(s)=1/s+2/s^2+2/s^3 2.1.3. f(t)=(1+2t+t^2)e^(-2t) ->F(s)=1/(s+2)+2/(s+2)^2+2/(s+2)^3 2.1.4. f(t)=e^t+e^(-t) ->F(s)=1/(s-1)+1/(s+1) ->F(s)=2s/(s^2-1) 2.1.5. f(t)=1/2(e^t-e^(-t)) (=sinh(t)) ->F(s)=1/2((1/(s-1)-1/(s+1)) ->F(s)=1/2((2/(s^2-1)) ->F(s)=1/(s^2-1) 2.1.6. f(t)=sin(2t)+3cos(2t) ->F(s)=2/(s^2+4)+3s/(s^2+4)=(2+3s)/(s^2+4) 2.1.7. f(t)=e^(-4t)[sin(2t)+3cos(2t)] ->F(s)=(2/(s+4^2+4))+(3(s+4)/((s+4)^2+4))=(3s+14)/(s^2+8s+20) Aufgabe 2.2 Berechnen Sie die Bildfunktion unter Verwendung des Integrals, welches die Laplace-Transformation definiert. 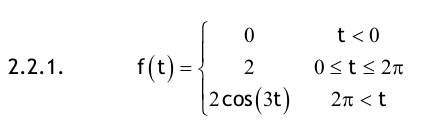 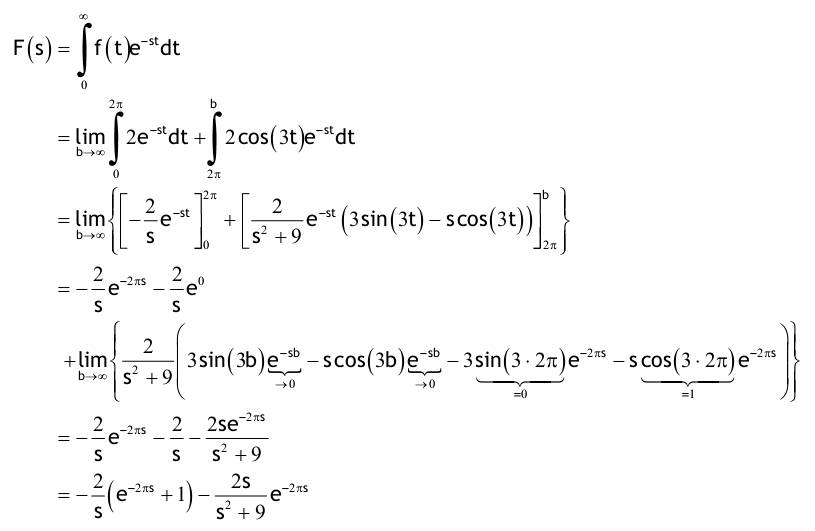  2.2.1. f(t)= (0; t<0) (2; 0<t<2π) (2cos(3t), 2π<t) F(s)=∫f(t)e^(-stdt wobei ∫ von 0 bis ∞ =lim∫(von 0 bis 2π)2e^(-st)dt+∫(von 2π bis b)2cos(3t)e^(-st)dt =lim(((-2/s)e^(-st))(von 0 bis 2π)+(2/(s^2+9)e^(-st)(3sin(3t)-scos(3t)))von 2π bis b) =(-2/s)e^(-2πs)-(2/s)e^0+lim(von b bis ∞)(2/(s^2+9)(3sin(3b)e^(-sb)-scos(3b)e^(-sb)-3sin(3*2π)e^(-2πs)-scos(3*2π)e^(-2πs)) =(-2/s)e^(-2πs)-2/s-(2se^(-2πs))/(s^2+9) 2.2.2. f(t)= (0, t<0) (A, 0<t<3) (Ae^(-t-3), 3<t) F(s)=∫f(t)e^(-st)dt wobei ∫ von 0 bis ∞ =lim∫Adt+∫Ae^(-t+3)e^(-st)dt=lim∫Adt+∫Ae^(-t(s+1)+1)dt =lim(((-A/s)e^(-st)+(-A/(s+1)e^(-t(s+1)+3))von 3 bis b =lim((-A/s)e^(-3s)+(A/s)e^0-A/(s+1)e^(-b(s+1)+3)+A/(s+1)e^(-3(s+1)+3)) =lim((-A/s)e^(-3s)+A/s-A/(s+1)e^(-b(s+1)+3)+A/(s+1)e^(-3s) =(-A/s)e^(-3s)+A/s+A/(s+1)e^(-3s) Aufgabe 2.3 Transformieren Sie mit der Tabelle der Laplace-Korrespondenzen vom Bild- in den Zeitbereich. Falls nötig, zerlegen Sie die Ausdrücke zunächst in Partialbrüche 2.3.1. F(s)=1/(s+2) I L^(-1) (..) -> f(t)=e^(-2t) 2.3.2. F(s)=5/(s+2) I L^(-1) (..) -> f(t)=5e^(-2t) 2.3.3. F(s)=2/(s^2-4) 2/(s^2-4)=A/(s+2)+B/(s-2) 2/(s^2-4)=(A(s-2)+B(s+2))/((s+2)(s-2)) Zählervergleich: 2=A(s-2)+B(s+2) 1. Weg: Nullstellen einsetzen: s=2->2=4B s=-2->-4A 2. Weg: Koeffizientenvergleich: s1:0=A+B s0: 2=-2A+2B A=-1/2; B=1/2 F(s)=(-1/2)1/(s+2)+(1/2)1/(s-2) I L^(-1)(..) f(t)=1/2(e^(2t)-e^(-2t)) f(t)=sinh(2t) 2.3.4. F(s)=2/(s^2+4) I L^(-1) (..) -> f(t)=sin(2t) 2.3.5. F(s)=s/(s^2+4) I L^(-1) (..) -> f(t)=cos(2t) 2.3.6. F(s)=s/(s^2-4) F(s)=s/(s^2-4) s/(s^2-4)=A/(s+2)+B/(s-2) s/(s^2-4)=((A(s-2)+B(s+2)))/(s+2)(s-2) Zählervergleich: s=A(s-2)+B(s+2) 1. Weg: Nullstellen einsetzen: s=2->2=4B s=-2->-2=-4B 2. Weg: Koeffizientenvergleich: s1:1=A+B s0:0=-2A+2B A=1/2; B=1/2 F(s)=1/2, 1/(s+2)+1/2, 1/(s-2) I L^(-1) (..) f(t)=1/2(e^(2t)+e^(-2t) f(t)=cosh(2t) 2.3.7. F(s)=1/(s+2)^2 F(s)=1/(s+2)^2 I L^(-1) (..) Dämpfungsregel f(t)=te^(-2t) |
| PDF Dokument Lösungen Laplace - Transformation |

