Version [72865]
Dies ist eine alte Version von TutoriumMathe3L2 erstellt von Jorina Lossau am 2016-10-06 10:03:18.
Tutorium Mathematik 3
Differentialgleichungen - Lösungen
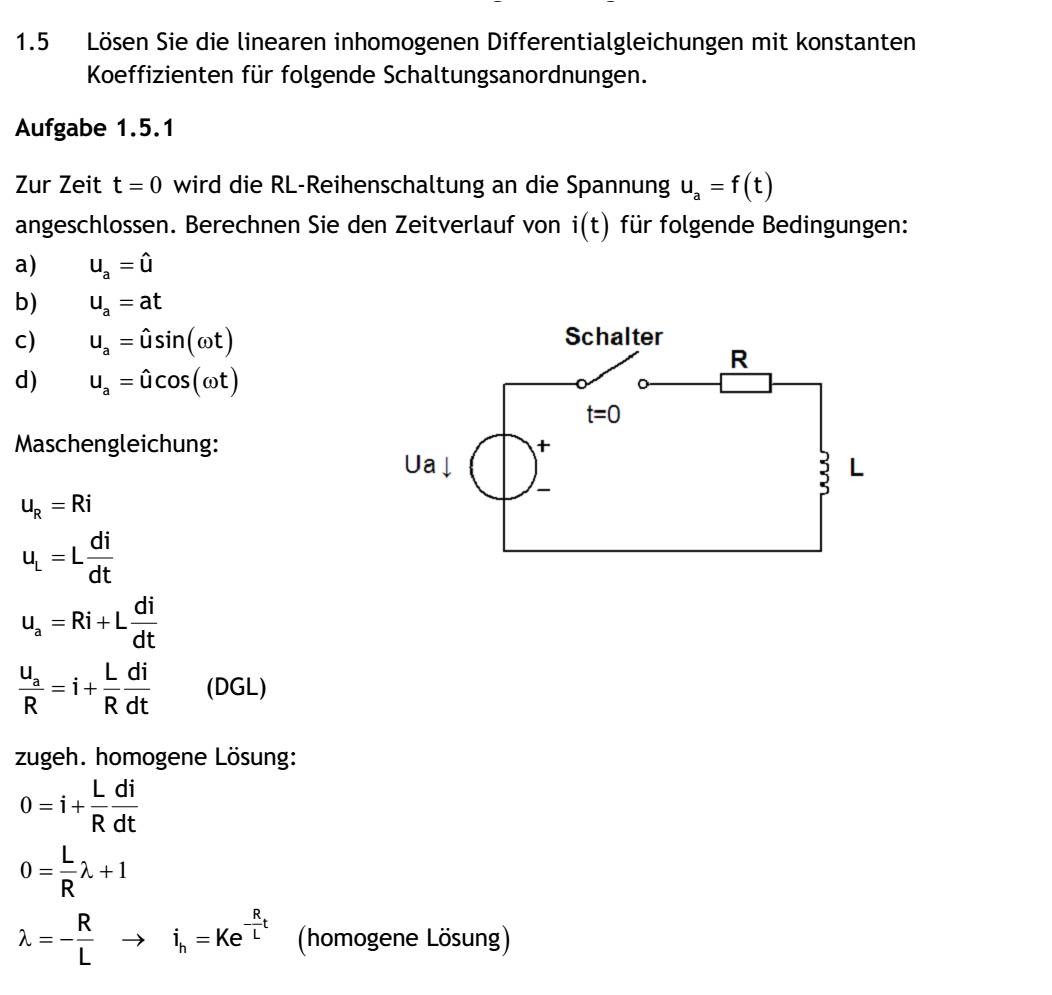




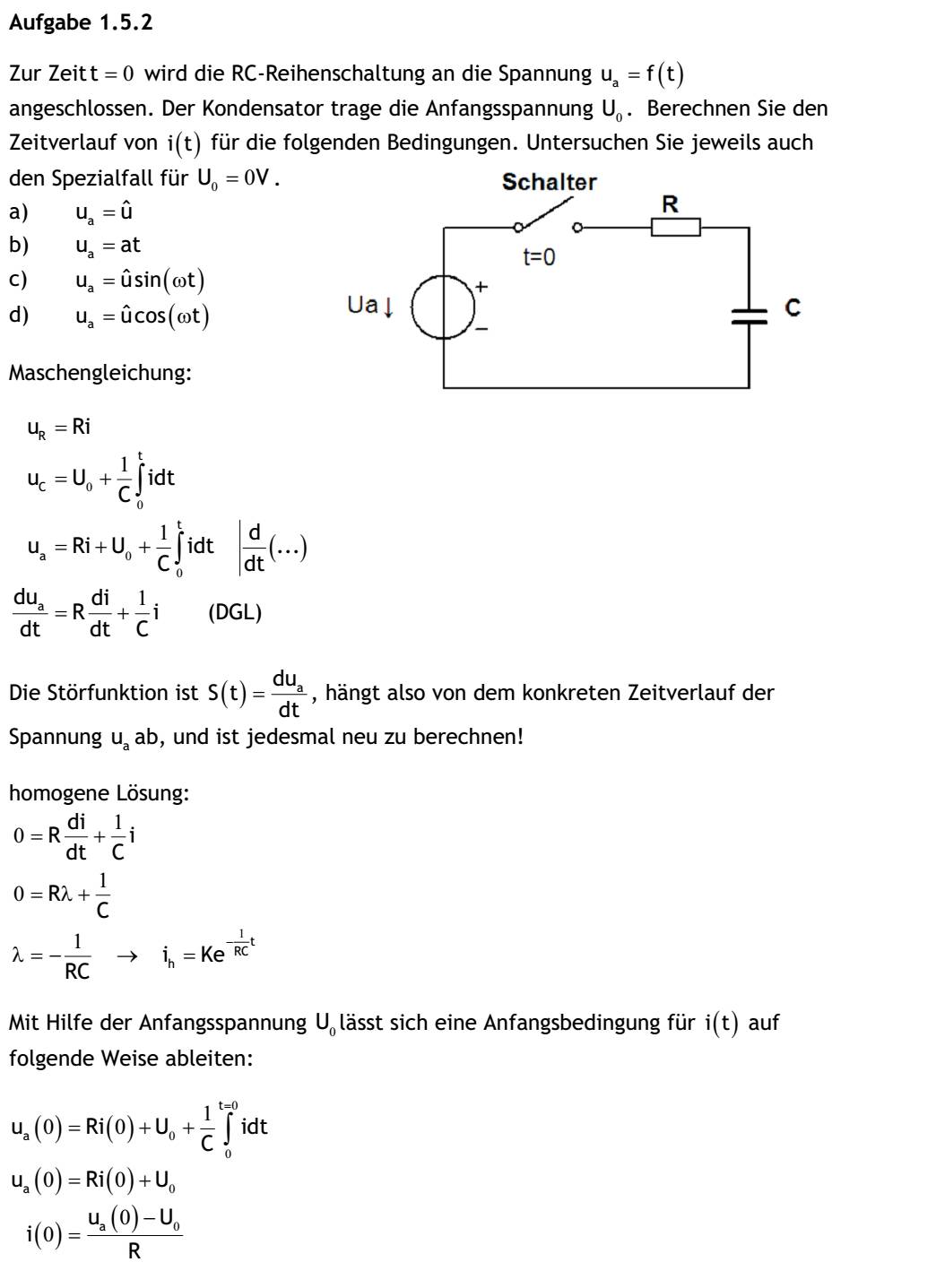
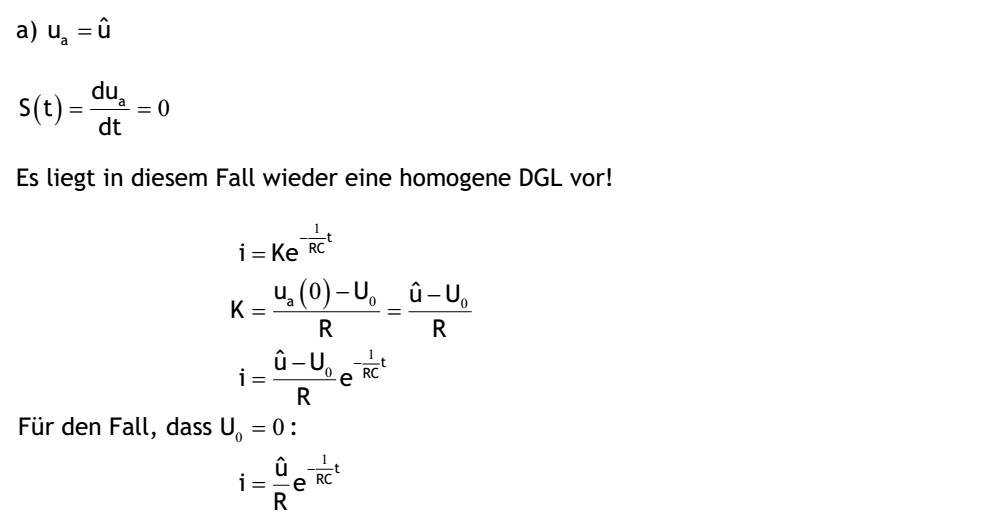


| 1.5 Lösen Sie die linearen inhomogenen Differentialgleichungen mit konstanten Koeffizienten für folgende Schaltungsanordnungen. Aufgabe 1.5.1 Zur Zeit t=0 wird die RL-Reihenschaltung an die Spannung Ua=f(t) angeschlossen. Berechnen Sie den Zeitverlauf von i(t) für folgende Bedingungen: a) ua=u^ b) ua=at c) ua=u^sin(wt) d) ua=u^cos(wt) Maschengleichung: uR=Ri uL=L(di/dt) ua=Ri+L(di/dt) ua/R=i+(L/R)*(di/dt) zugeh. homogene Lösung: 0=i+(L/R)*(di/dt) U=(L/R)λ+1 λ=-R/L->ih=ke^((-R/L)t) (hom. Lösung) a) Ua=u^ partikuläre Lösung: u^/R=i+(L/R)*(di/dt) ip=A dip/dt=0 ip, dip/dt in DGL: u^/R=A+(L/R)*0 A=u^/R ip=u^/R i=ih+ip i=ke^((R/L)*t)+u^/R mit Anfangsbed. i(0)=0 0=K+u^/R K=-u^/R i(t)=-(u^/R)e^((R/L)t)+u^/R b) ua=at partikuläre Lösung: at/R=i+(L/R)*(di/dt) ip=At+B dip/dt=A ip,dip/dt in DGL: at/R=At+B+(L/R)*A t:A=a/R t0:0=B+(L/R)*A -> 0=B+(L/R)*(a/R)-> B=-La/R^2 ip=(a/R)*t-La/R^2 i=ih+ip i=ke^((R/L)*t)+(a/R)*t-(La)/(R^2) mit Anfangsbedingung i(0)=0 0=K-La/R^2 K=La/R^2 i(t)=(a/R)t-La/R^2(1-e^((-R/L)t) c) ua=u^sin(ωt) partikuläre Lösung: (u^sin(ωt))/R=i+(L/R)*(di/dt) ip=Acos(ωt)+Bsin(ωt) dip/dt=-Aωsin(wt)+Bωcos(ωt) ip, dip/dt in DGL: (u^sin(ωt))/R=Acos(ωt)+Bsin(ωt)+L/R(-Aωsin(ωt)+Bωcos(ωt)) sin(ωt): 1: u^/R=B-(LAω)/R cos(ωt): 2: 0=A+(LBω)/R nach Lösung des GLS: A=(-Lωu^)/((Lω)^2+R^2), B=Ru^/((Lω)^2+R^2) ip=(-Lωu^)/((Lw)^2+R^2)cos(ωt)+Ru^/((lω)^2+R^2)sin(ωt) i=ih+ip i=ke^(-R/L)*t)-Lωu^/((Lω)^2+R^2)cos(ωt)+Ru^/((Lω)^2+R^2)sin(ωt) |
| PDF Dokument Lösungen Differentialgleichungen |

