Tutorium Mathematik 3
Anwendungen der Integralrechnung - Lösungen
| Aufgaben und Lösungen |
|---|
| 1) Eine Kette wird zwischen zwei gleich hohen Aufhängepunkten im Abstand l = 5 m befestigt. Gegenüber diesen Punkten hängt sie in der Mitte um d = 3 m durch. Wie lang ist die Kette? 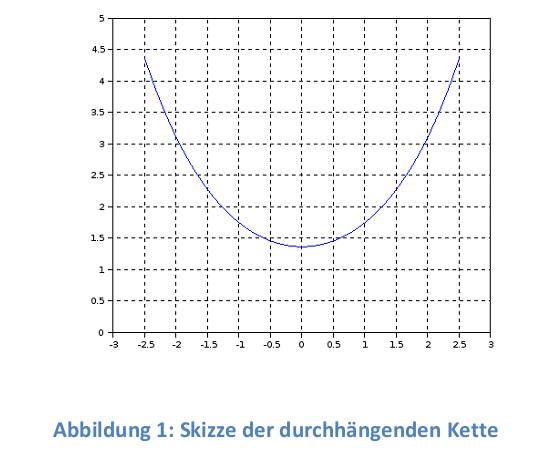 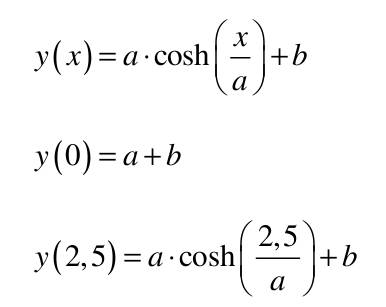 y(x)=a*cosh(x/a)+b y(0)=a+b y(2,5)=a*cosh(2,5/a)+b Die Kette hängt um d = 3m durch 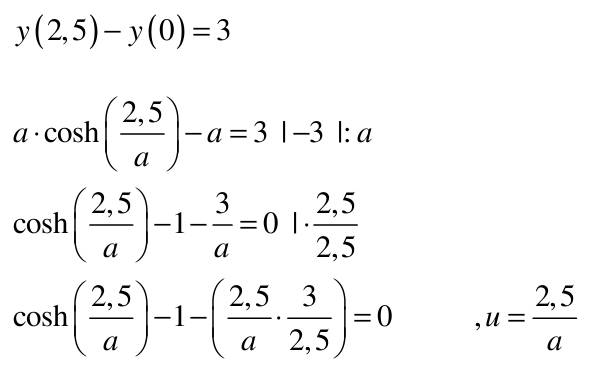 y(2,5)-y(0)=3 a*cosh(2,5/a)-1-(2,5/a)-1-3/a=0 I* 2,5/2,5 cosh(2,5/a)-1-(2,5/a*3/2,5)=0; u=2,5/a Nach der Substitution u = 2,5/a kann mit dem Newton-Verfahren die Nullstelle gesucht werden: 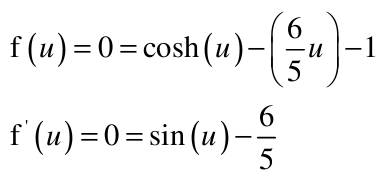 f(u)=0=cosh(u)-(6/5u)-1 f'(u)=0=sin(u)-6/5 Mit un=2 ergibt sich nach wenigen Iterationen u = 1,82937 und somit a = 2,5/u = 1,3666. Damit ist die Funktion, welche die Kettenlinie beschreibt eindeutig definiert und es kann die Bogenlänge berechnet werden. 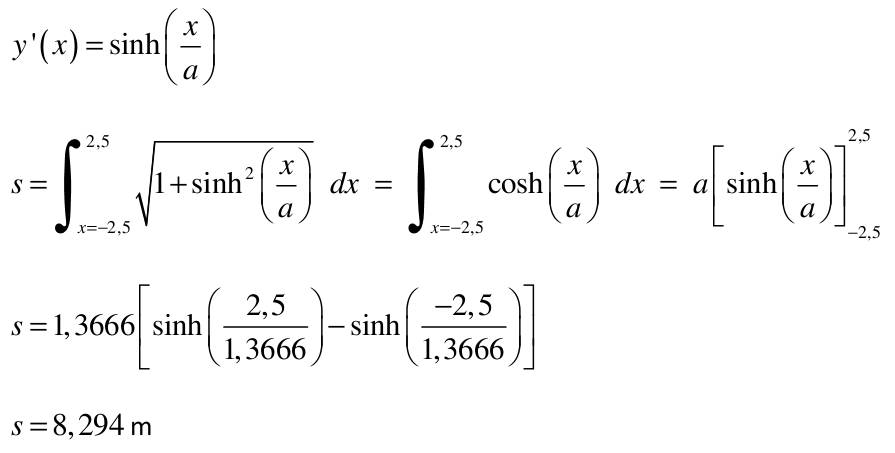 y'(x)=sinh(x/a) s=∫√(1+sinh^2(x/a))dx wobei ∫ von x=-2,5 bis 2,5 =∫cosh(x/a)dx=a(sinh(x/a)) wobei ∫ von -2,5 bis 2,5 s=1,3666(sinh(2,5/1,3666)-sinh(-2,5/1,3666) s=8,294m 2) Ein Parabolspiegel wird durch die Rotation der Kurve y = k *x² um die y-Achse beschrieben. Wie groß ist seine Oberfläche für k = 1 / m = und 0 ≤ x ≤ 1 m (der Parabolspiegel hat also damit einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m).Vergleichen Sie die berechnete Oberfläche mit der einer Halbkugel vom Radius r = 1 m (Die Halbkugel hat auch einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m). mit k = 1 und y`(x) = 2x 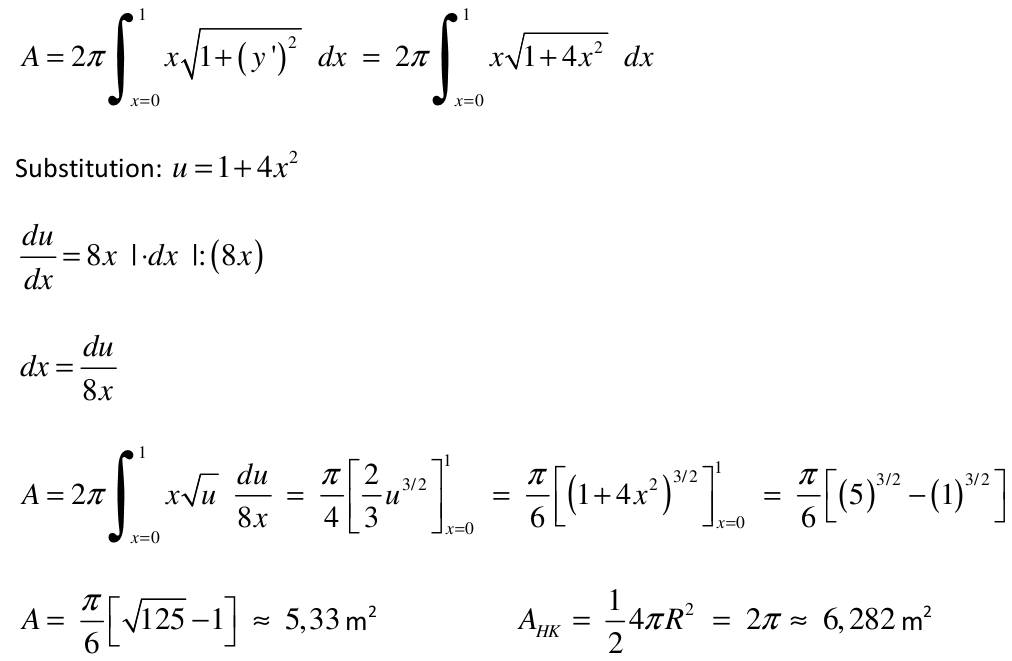 A=2π∫x√(u)du/8x wobei ∫ von x=0 bis 1 =π/4(2/3u^3/2) von x=0 bis 1 = π/6((1+4x^2)^3/2) von x=0 bis 1 =π/6((5)^3/2-(1)^3/2) A=π/6(√125-1)= rund 5,33m^2 AHK=1/2uπR^2=2π =rund 6,282m^2 3) Während der Zeit T falle ein Strom gemäß einer e-Funktion vom Wert ˆi auf seine Hälfte. Berechnen Sie den integralen Mittelwert und den Effektivwert dieses Stroms in der Zeit T.  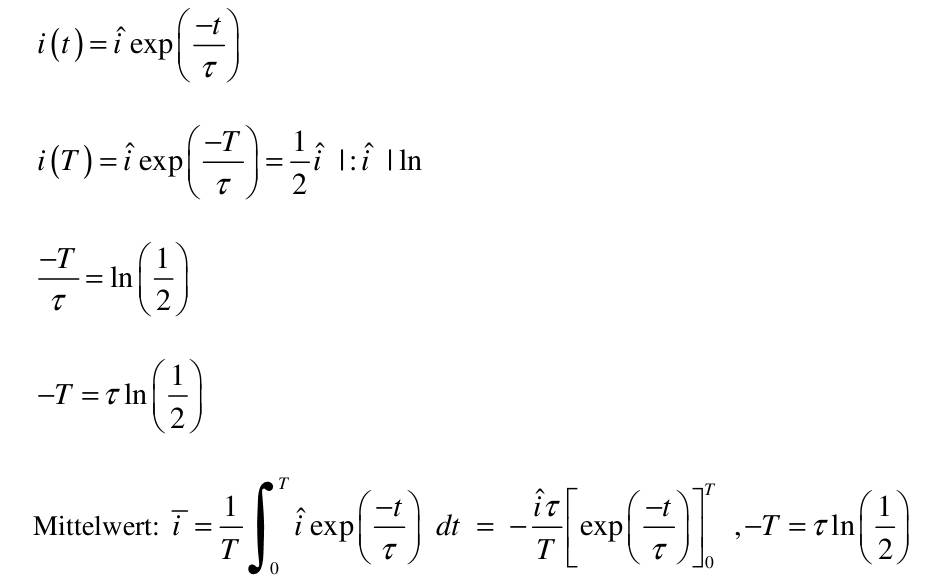 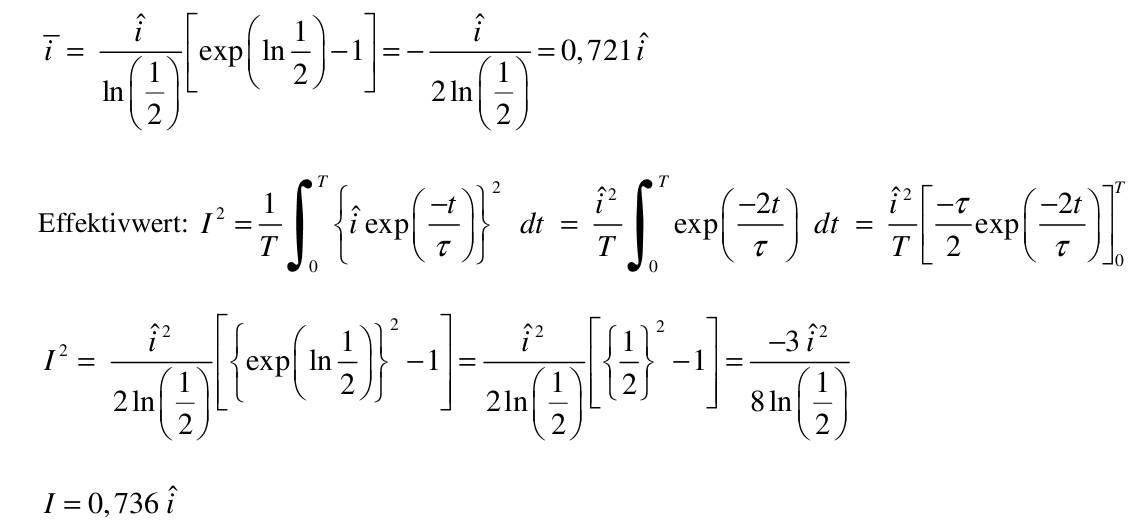 i(t)=iexp(-t/г) i(T)=iexp(-T/г)=1/2i I:iI ln -T/г=ln(1/2) -T=гln(1/2) Mittelwert: T=1/T∫iexp(-t/г)dt wobei ∫ von 0 bis T =ir/T(exp(-t/r) von 0 bis r, -T=rln(1/2) i=i/ln(1/2)(exp(ln1/2)-1)=-i/(2ln1/2)=0,721i Effektivwert: I^2 =1/T∫(iexp(-t/г))^2dt wobei ∫ von 0 bis T=i^2/г∫exp(-2t/г)dt wobei ∫ von 0 bis T =i^2/T(-г/2exp(-2t/г)) von 0 bis r I^2=i^2/(2ln(1/2))((exp(ln1/2))^2-1)=i^2/(2ln(1/2))((1/2)^2-1)=-3i^2/(8ln(1/2)) I=0,736i 4) Ein Körper entsteht durch die Rotation der Kurve sin y Wurzel von x um die x-Achse, wobei gilt: 0 ≤ x ≤ π . Berechnen Sie das Volumen des Körpers. Hinweis: Verwenden Sie für das zu lösende Integral die partielle Integration, wobei Sie die Stammfunktion von sin²x aus dem Tabellenbuch entnehmen. 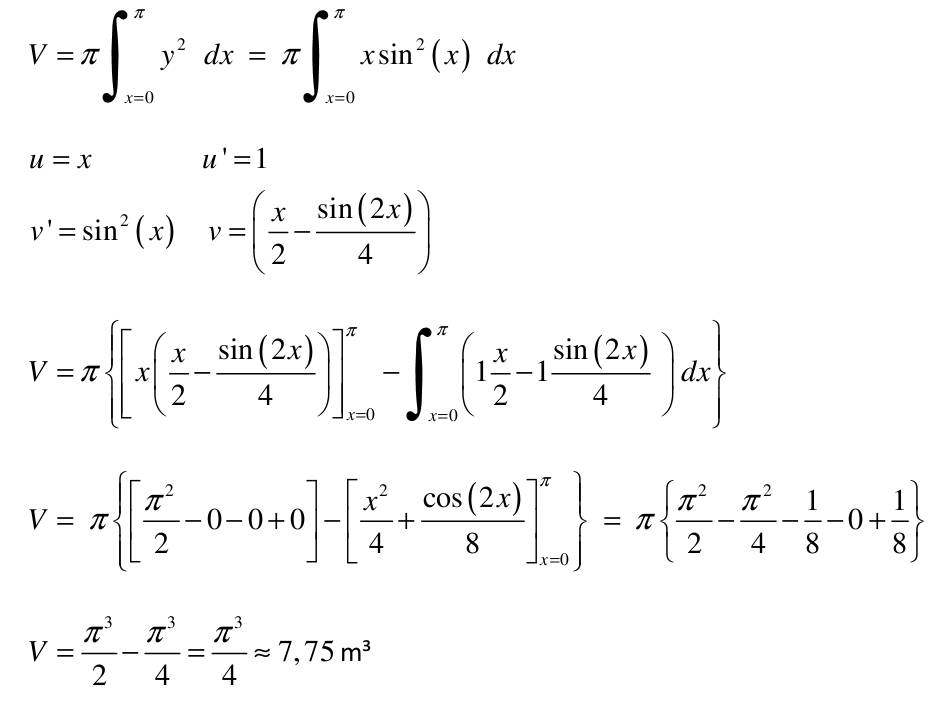 V=π∫y^2dx wobei ∫ von x=0 bis π =π∫xsin^2(x)dx wobei ∫ von x=0 bis π u=x u'=1 V'=sin^2(x) V=(x/2-((sin2x)/4)) V=π((x(x/2-(sin2x/4)) von x=0 bis π - ∫(1x/2-1sin2x/4)dx) wobei ∫ von x=0 bis π V=π((π^2/2-0-0+0)-(x^2/4+cos(2x)/8) von x=0 bis π =π(π^2/2-π^2/4-1/8-0+1/8) V=π^3/2-π^3/4=π^3/4=rund 7,75m^3 |
| PDF Dokument Lösungen Integralrechnung |

