Version [58505]
Dies ist eine alte Version von TutoriumMathe3KlausurL erstellt von Jorina Lossau am 2015-08-30 11:51:03.
Tutorium Mathematik 3
| File | Last modified | Size |
|---|---|---|
| Mathe1L.jpg | 2023-10-06 18:37 | 5Kb |
| Mathe3KlausurL.pdf | 2023-10-06 18:37 | 84Kb |
| Mathe3L111.jpg | 2023-10-06 18:37 | 47Kb |
| Mathe3L112.jpg | 2023-10-06 18:37 | 70Kb |
| Mathe3L113.jpg | 2023-10-06 18:37 | 41Kb |
| Mathe3L114.jpg | 2023-10-06 18:37 | 61Kb |
| Mathe3L115.jpg | 2023-10-06 18:37 | 48Kb |
| Mathe3L116.jpg | 2023-10-06 18:37 | 92Kb |
| Mathe3L117.jpg | 2023-10-06 18:37 | 29Kb |
| MatheL10.jpg | 2023-10-06 18:37 | 37Kb |
| MatheL11.jpg | 2023-10-06 18:37 | 22Kb |
| MatheL12.jpg | 2023-10-06 18:37 | 21Kb |
| MatheL2.jpg | 2023-10-06 18:37 | 1Kb |
| MatheL3.jpg | 2023-10-06 18:37 | 3Kb |
| MatheL4.jpg | 2023-10-06 18:37 | 5Kb |
| MatheL5.jpg | 2023-10-06 18:37 | 5Kb |
| MatheL6.jpg | 2023-10-06 18:37 | 5Kb |
| MatheL7.jpg | 2023-10-06 18:37 | 7Kb |
| MatheL8.jpg | 2023-10-06 18:37 | 3Kb |
| MatheL9.jpg | 2023-10-06 18:37 | 22Kb |
Beispielklausur - Lösungen
1. Berechnen Sie das zweifache Integral über das rechteckige Gebiet G mit  Lösung: 3 2. Gegeben ist die Funktion y(t) = e^2t im Intervall [0; 0,5]. 2.1 Berechnen Sie den integralen Mittelwert in diesem Intervall! Lösung: 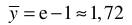 Denken Sie sich diese Funktion periodisch mit T = 0,5 fortgesetzt und bestimmen Sie für diesen Fall den Effektivwert. 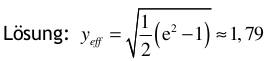 3. Man bestimme die allgemeine Lösung der Differentialgleichung mit Hilfe des λ -Ansatzes und einem geeigneten Ansatz für die partikuläre Lösung : y’’ + 10y’ + 34y = sin(x) 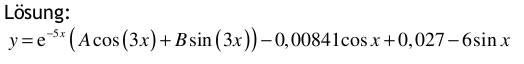 4. Aufgabe: Laplace - Transformation 4.1. Transformieren Sie unter Verwendung von Korrespondenztabellen folgende Funktionen vom Zeit- in den Bildbereich: a) f(t) = 4e^ -t b) f(t) = t*e^ -5t c) f(t) = 5cos (8t) Lösung: 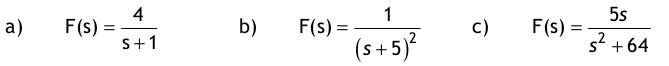 4.2. Transformieren Sie unter Verwendung von Korrespondenztabellen die Bildfunktionen in den Zeitbereich: 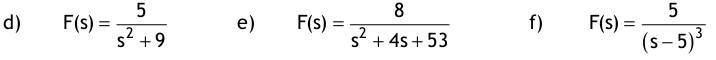 4.3. Lösen Sie die nachfolgende Anfangswertaufgabe mit Hilfe der Laplacetransformation : 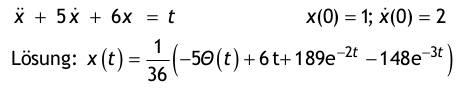 5. Man löse die inhomogene Differentialgleichung mittels Variation der Konstanten: y' - 2y = x* e ^ 2x 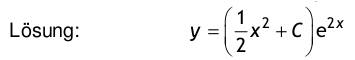 6. Fourier - Reihen 6.1. Gegeben sind 3 Funktionen y = f(t) mit der Periodendauer T = 2π durch einen nur im Intervall [-π; π] zutreffenden Ausdruck. Fertigen Sie von allen drei Funktionen eine Skizze für den Bereich t ∈ [-3π ; 3π ] an : a) y = | t |+ t in [-π ; π ] T = 2π 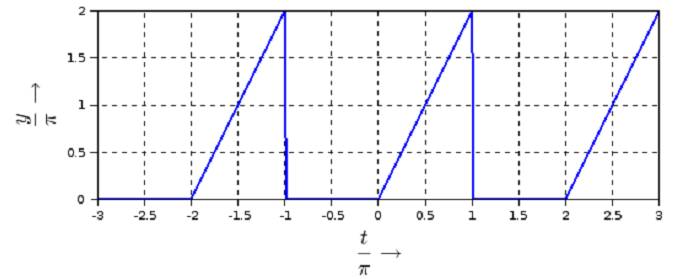 b) y = t^2 in [-π ; π ] T = 2π 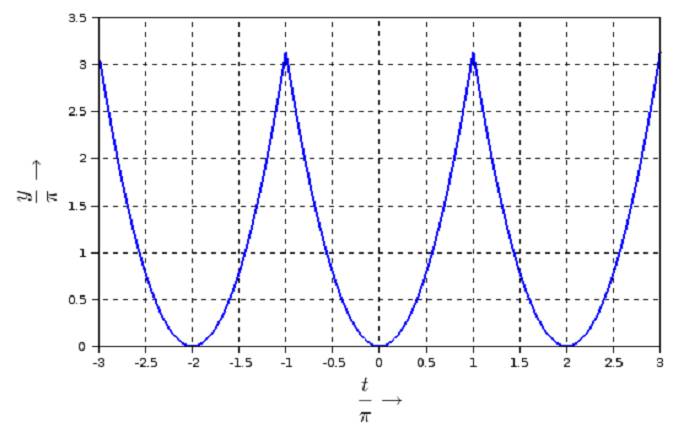 c) y = sin (t/2) in [-π ; π ] T = 2π 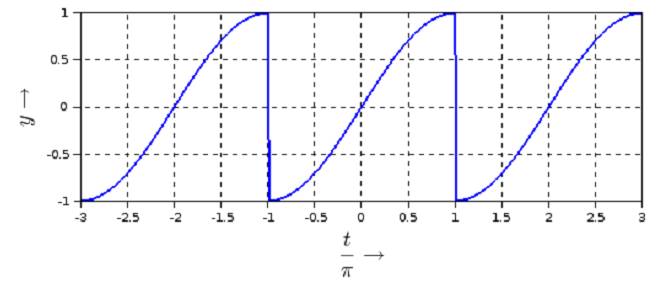 6.2. Bestimmen Sie für alle drei Funktionen den Gleichanteil a0/2 und tragen ihn in die Tabelle ein. Untersuchen Sie, ob die Koeffizienten der reellen Fourierreihe an (cos - Anteile) bzw. bn (sin - Anteile) Null sind, und vermerken das in der nachfolgenden Tabelle durch ja oder nein.  |

