Version [59015]
Dies ist eine alte Version von TutoriumMathe3DGL erstellt von Jorina Lossau am 2015-09-07 11:40:00.
Tutorium Mathematik 3
| File | Last modified | Size |
|---|---|---|
| DGL1.jpg | 2023-10-06 18:37 | 1Kb |
| DGL2.jpg | 2023-10-06 18:37 | 2Kb |
| DGL3.jpg | 2023-10-06 18:37 | 3Kb |
| DGL4.jpg | 2023-10-06 18:37 | 5Kb |
| DGL5.jpg | 2023-10-06 18:37 | 14Kb |
| Mathe3DGL.jpg | 2023-10-06 18:37 | 137Kb |
| Mathe3DGL.pdf | 2023-10-06 18:37 | 307Kb |
Einfach integrierbare DGL
| In der ersten elektrischen Schaltung genügen die Ströme prinzipiell dem Knotensatz und die Spannungen der Maschenregel, und zwar auch wenn sich Ströme und Spannungen mit der Zeit verändern. Betrachtet man den eingeschwungenen Zustand und sinusförmige Wechselspannungen, so lassen sich die Verhältnisse gut mit dem Formalismus der komplexen Zahlen beschreiben. Zur korrekten Beschreibung von Schaltvorgängen und von Einschwingvorgängen sind die Spannungen an ohmschen Widerständen R, an Induktivitäten L, und Kapazitäten in Abhängigkeit von Strom i(t) wie folgt zu beschreiben: Spannung an ohmschen Widerstand: 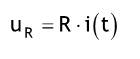 Spannung an Induktivität: 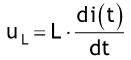 Spannung an Kapazität: 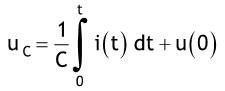 Wegen des Integrals uc erhält man eine Differentialgleichung erst nach Differentation nach der Zeit t. Dabei wird ausgenutzt, dass das Differenzieren nach t das Integral mit der oberen Grenze t wieder aufhebt. |
| PDF Dokument Differentialgleichungen |

