Projekt Einsparzähler - Bwl202FinanzmathematischeGrundlagen

• Startseite
• über das Projekt
• IFE

Betriebswirtschaftslehre 2 - Investitionsrechnung und Finanzierung - Kapitel 2 - Finanzmathematische Grundlagen

Inhalte von Prof. Dr. Thomas Urban
www.multi-media-marketing.org

2.1 Finanzmathematische Grundlagen

2.1.1 Einfache Verzinsung

• Zinsen sind die Vergrößerung eines Betrages in einer bestimmten definierten Zeit, der Zinsperiode

• Maß der Verzinsung ist durch den Zinssatz gegeben

• wegen der anzutreffenden unterschiedlichen Zinszuschreibungsmodalitäten resultieren aus einem bestimmten nominellen Jahreszinssatz durchaus verschiedene s. g. effektive Jahreszinssätze

• bei Zinsrechnungen werden Zahlungen auf einen einheitlichen Zeitpunkt bezogen und zu diesem Zeitpunkt verglichen

• entweder zum Zeitpunkt t₀ oder zum Ende der Zinsvereinbarung (Zeitpunkt n), d. h. nach n Perioden

• wird im Zeitraum t₀ ein Betrag K₀ zur Verfügung gestellt, so sind die zu zahlenden Zinsen Z proportional zur Zeit t und proportional zum Kapital K₀

• der Proportionalitätsfaktor heißt Zinssatz i (Einheit % p. a.)

• Wenn die Zinsen am Ende des Zeitraumes dem Kapital zugeschlagen werden, dann beträgt das Kapital nach n Jahren:

• Ksub> = K₀ + (K₀ * i) + ... + (K₀ * i) = K₀ + (K₀ * i * n) = K₀ * (1 + i * n)

• n = Anzahl der Perioden

• i = Jahreszinssatz

• die Zinsen können auch in Abhängigkeit von der Zahl der Tage T angeben werden, wobei das Jahr im allgemeinen zur rechnerischen Vereinfachung 360 Tage gerechnet wird T = Zahl der Tage; 1 Jahr = 360 Tage

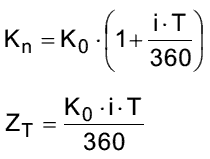
2.1.2 Zinseszinsrechnung

Jährliche Zinszuschreibung

• ein zum Zeitpunkt t₀ verfügbarer Kapitalbetrag K₀ werde zum Zinssatz i angelegt, der als Jahreszinssatz definiert ist.

• nach genau 1 Jahr und der entsprechenden Zinszuschreibung ist der Kapitalbetrag K₁ vorhanden mit

• K₁ = K₀ + i * K₀ = K₀ * (1 + i)

• nach genau 2 Jahren beträgt der vorhandene Kapitalbetrag K₂

• K₂ = K₁ + i * K₁ = K₁ * (1+i) = K₀ * (1 + i)²

• nach genau n Jahren ist der Betrag K_n vorhanden mit

• K_n = K_n-1 + i * K_n-1 = K_n-1 * (1 + i) = K₀ * (1 + i)ⁿ

• nach einer Anlagedauer von n Jahren ergibt sich ein nach dieser Zeit erzielter, zum Zeitpunkt n vorliegender Endwert E_n in Abhängigkeit von der Größe n des Betrachtungszeitraumes zu

• E_n = K_n = K₀ * (1 + i)ⁿ = K₀ * qⁿ

Beispiel:

• Bezogen auf die Geldanlage (Sparbrief) beträgt der Endwert E₂

• E₂ = K₂ = 1.000 * (1 + 0,05)² = 1.102,50

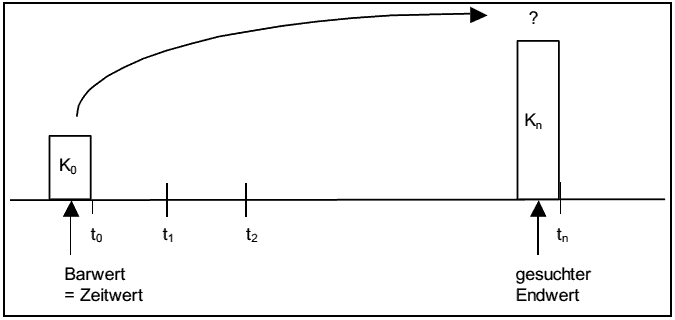
Aufzinsung in der Kaufmännischen Verzinsung

• Auflösung der Zinsformel nach dem Betrag K₀ erlaubt den Vergleich der gleichwertigen Investitionssummen ⇒ Formel für den "Barwert" eines in der Zukunft fälligen Betrages:

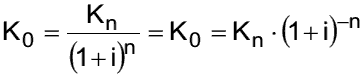
• Bei der Abzinsung (= Diskontierung) liegt die Fragestellung zugrunde, wie viel ein Kapitalbetrag K_n, der am Ende des Jahres n anfällt, zu Beginn des Planungszeitraums wert ist.

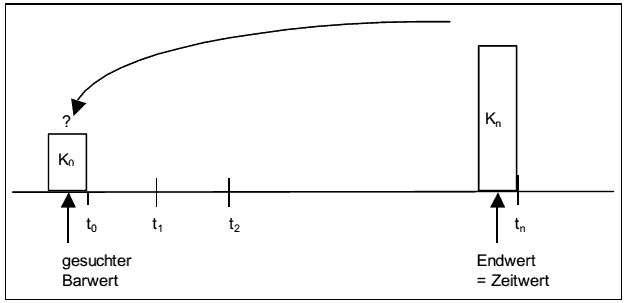
Abzinsung in der Kaufmännischen Verzinsung


Um bei gegebenem Zinssatz i die Dauer n zu ermitteln, verwendet man folgende Beziehung:



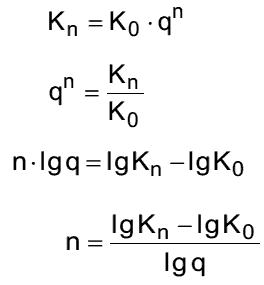
Die Verzinsung i, die bei einer bestimmten Laufzeit n notwendig ist, um von K₀ aus K_n zu erreichen, kann folgendermaßen ermittelt werden:

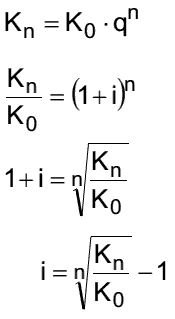
Unterjährige Verzinsung

• Begriffe werden gern durcheinander gebracht!

• wenn bei Zinseszinsrechnungen der Zuschlag der angelaufenen Zinsen auf das Kapital zu mehreren Terminen gleichen Abstandes im Jahr erfolgt ⇒ unterjähriger Verzinsung

• relativen unterjährigen Zinssatz i_rel ⇒ Jahreszins i wird in so viele Teile m geteilt, wie Termine pro Jahr gesetzt sind

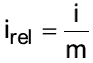
• Der Jahreszinssatz i ist dann nicht mehr wirksam und wird daher als nominelle Verzinsung dieses Jahres bezeichnet. Die effektive Verzinsung i_eff ergibt z. B. bei zwei Terminen pro Jahr:

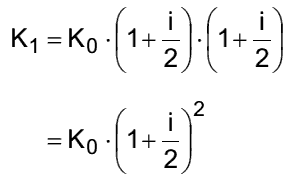
• Bei m Terminen gilt:

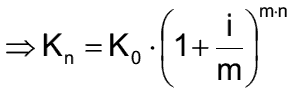
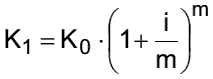
• Dieses K_n ist größer als das entsprechende bei jährlichem Zinszuschlag.

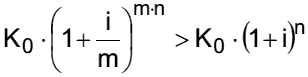
Anwendung des relativen unterjährigen Zinssatzes i_rel ergibt gegenüber dem nominellen Zinssatz i eine höhere effektive Jahresverzinsung i_eff



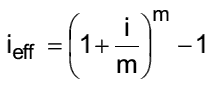
Ermittlung des nominellen Zinssatzes aus der effektiven Jahresverzinsung:

Gemischte Verzinsung

• wenn der Verzinsungszeitraum nicht nur aus ganzen Berechnungsperioden (Jahren) besteht, sondern auch aus Bruchteilen davon ⇒ gemischte Verzinsung vorgenommen

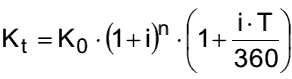
• Liegen die unvollständigen Zinsperioden am Anfang und am Ende der Laufzeit, ergibt sich folgende Berechnung:

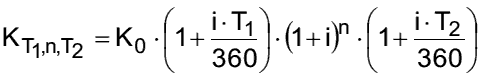
• Die Ermittlung des Barwertes K₀ ergibt sich bei gemischter Verzinsung demzufolge als:

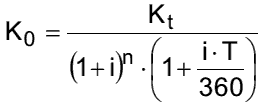
Stetige Verzinsung

• Bei gleichem Nominalzinssatz steigt die effektive Verzinsung mit der Häufigkeit der unterjährigen Zinstermine.

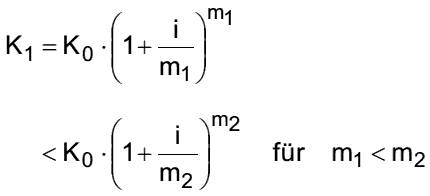
• für möglichst hohe Verzinsung ⇒ sehr weitgehende Aufteilung der Zinsperiode anstreben

• K₁ wird maximal für m ⇒ ∞; m = unterjährige Zinstermine

• wenn m ⇒ ∞ gesetzt wird, dann folgt:

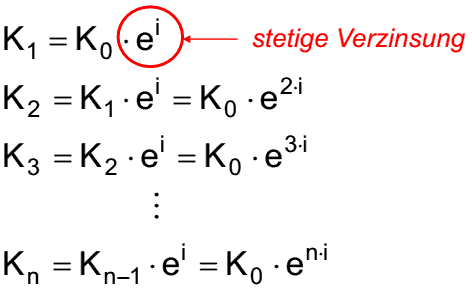
• effektiver Jahreszins i_eff bei stetiger Verzinsung:

• K₀ * (1 + i_eff) = K₁ * eⁱ

• 1 + i_eff = eⁱ

• i_eff = eⁱ - 1

Beispiel
• Welchen Betrag besitzt ein Guthaben von 1.000 € nach Ablauf eines Jahres, wenn es
a) jährlich mit 12 %,
b) vierteljährlich mit 3 %,
c) monatlich mit 1 %,
d) an 360 Zinstagen täglich mit 12/360 %,
e) stetig mit einer Momentanverzinsung von 12 % verzinst wird?

2.2 Barwert und Endwert

• Kapitalbeträge zum Zeitpunkt t = 0 durch Auf-(Ver-)zinsung zu einem Endwert in t = n überführt oder aus einem Endkapital durch Abzinsung (Diskontierung) das Anfangskapital ermittelt werden

• unterschiedliche Anlage- oder Kreditformen können miteinander verglichen werden ⇒ nicht nur einzelne Zahlungen sondern auch Zahlungsströme

• Ein Zahlungsstrom ist dadurch charakterisiert, dass zum Zeitpunkt t Einzahlungen E_t und/oder Auszahlungen A_t erfolgen, die als Periodenüberschuss (periodische Nettozahlung) P_t zusammengefasst werden können.

• Erfolgt die Diskontierung der Differenz der periodischen Ein- und Auszahlungen mit q^-n (Diskontierungsfaktor) auf einen Bezugszeitpunkt, wird dieser Betrag als Barwert BW des Zahlungsstroms bezeichnet.

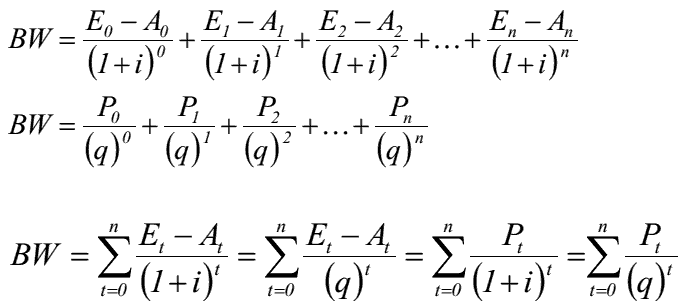
Beispiel

• Wie hoch sind die Barwerte der nachfolgenden Zahlungsreihen (alle Werte in €), wenn für Zahlungsreihe (ZR) I ein Zinssatz von 5% p. a. und für Zahlungsreihe II ein Zinssatz von 6% p. a. gilt?




• Erfolgt eine Aufzinsung der Differenz der jährlichen Ein- und Auszahlungen (Nettozahlungen) mit q^-n (Aufzinsungsfaktor), wird der sich ergebende Betrag als Endwert E_-n des Zahlungsstroms bezeichnet.




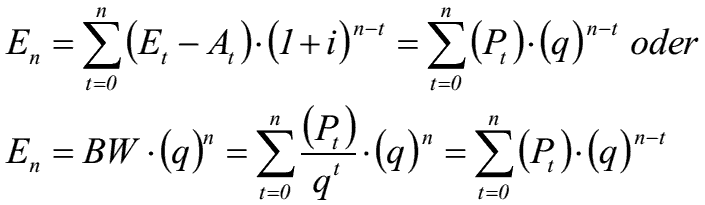
Beispiel

• Wie hoch sind die Endwerte der nachfolgenden Zahlungsreihen (alle Werte in €), wenn für Zahlungsreihe (ZR) I ein Zinssatz von 5% p. a. und für Zahlungsreihe II ein Zinssatz von 6% p. a. gilt?

2.3 Rentenrechnung

• Renten stellen regelmäßig wiederkehrende Zahlungen dar, d. h. die Dauer der Zahlungen (Rentendauer) muss mindestens über zwei Perioden gehen.

Merkmale der Rentenzahlungen

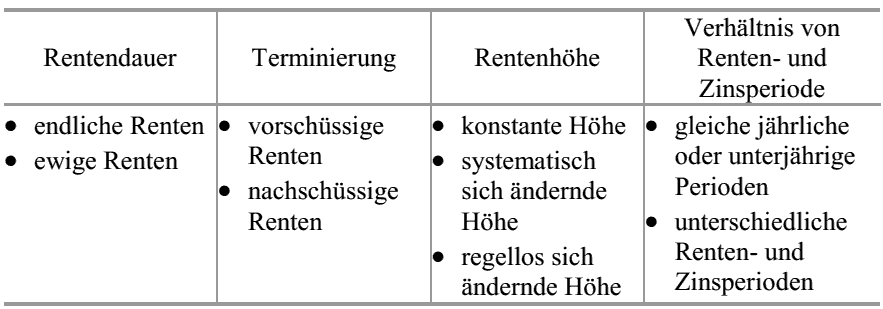
2.3.1 Konstante jährliche nachschüssige Rentenzahlungen mit jährlichen Zinsen

• Periodenzahlungen identischer Höhe = Rente r

• bei der nachschüssigen Rente erfolgt der Zahlungsfluss immer am Ende einer Periode und wird ab diesem Zeitpunkt über eine Laufzeit von n Jahren mit einem Jahreszinssatz i sowie Zinseszins verzinst

• Rentenbarwert R_-0 berechnet sich als Summe der Barwerte der einzelnen Rentenzahlungen

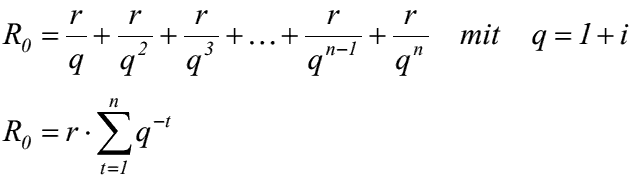
• bei dem Term 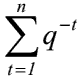handelt es sich um eine Aufsummierung von Diskontierungsfaktoren

• Der Ausdruck 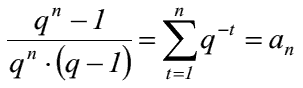wird nachschüssiger Rentenbarwertfaktor (RBF) genannt.

• Der Rentenbarwertfaktor hängt vom Zinssatz i und der Laufzeit n ab.

• Der Kapitalwert entspricht dem Rentenbarwert: C₀ = R_-0

• Rentenbarwert

.

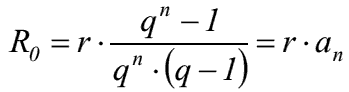
• Rentenendwert R_n = Summe aller Rentenzahlungen und ihrer zugehörigen Zinsen und Zinseszinsen am Ende der Laufzeit

• Rentenendwert ergibt sich als Aufzinsung des Rentenbarwertes mit der Formel der Zinsrechnung:

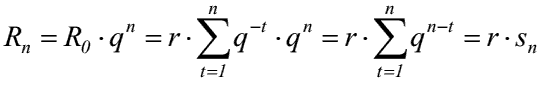
• nachschüssiger Rentenendwertfaktor (REF) wird funktional wie folgt beschrieben:

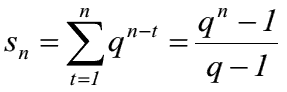
Berechnung der Rentenhöhe und der Laufzeit bei nachschüssiger Terminierung

2.3.2 Konstante jährliche vorschüssige Rentenzahlungen mit jährlichen Zinsen

• bisheriger Ansatz: Rentenzahlungen erfolgen jeweils am Ende eines Jahres

• allerdings können diese auch zu Beginn des Jahres stattfinden und werden ab diesem Zeitpunkt mit dem jeweiligen Jahreszinssatz zinseszinslich verzinst

• Rentenbarwert einer vorschüssig gezahlten Rente:

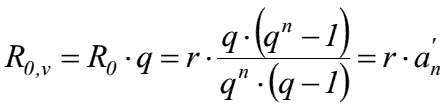
• vorschüssiger Rentenbarwertfaktor: Symbol a'_n

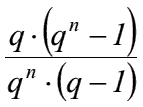
• analog zum vorschüssigen Rentenbarwert hat die zeitliche Verschiebung der Zahlungen um eine Periode nach vorn, die gleiche Auswirkung auf den zugehörigen Rentenendwert

• der vorschüssige Rentenendwert ergibt sich somit als der um eine Periode aufgezinste nachschüssige Rentenendwert

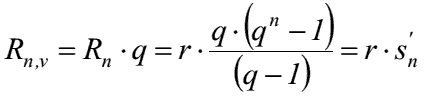
• vorschüssiger Rentenbarwertfaktor: Symbol s'_n

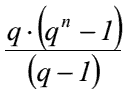
Berechnung der Rentenhöhe und der Laufzeit bei vorschüssiger Terminierung

2.3.3 Ewige Renten

• Wenn für die Laufzeit einer Rentenzahlung n ⇒ ∞ gilt, wird dies als ewige Rente bezeichnet. Die ewige Rente entspricht somit den Zinsen des Kapitals.

• Bestimmung eines Rentendwertes ist aufgrund der nie endenden Laufzeit nicht möglich

• Welche Auswirkung n ⇒ ∞ auf den nachschüssigen Rentenbarwert?

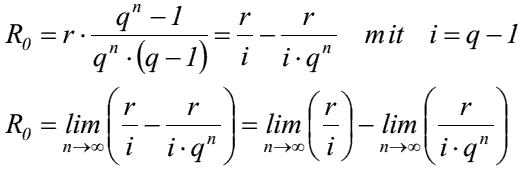
• für den Rentenbarwert R'_0,∞ einer ewigen nachschüssigen Rente folgt:

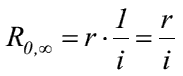
• wie zu sehen war, erfuhr der vorschüssige Rentenbarwert gegenüber dem nachschüssigen Ansatz die Erweiterung um eine periodische Verzinsung

• dies für die ewige Rente angewandt, folgt für den vorschüssigen Rentenbarwert R'₀, v, ∞:

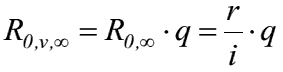
2.4 Annuitätenrechnung

• Leitgedanke der Annuitätenrechnung besteht darin, Zahlungen gleichmäßig auf die Nutzungsjahre eines Investitionsobjektes zu verteilen

• Annuitätenrechnung aus Finanzierungssicht

• wenn für die Durchführung einer Investition eine Schuld (Darlehen, Kredit) aufgenommen wurde, muss diese entsprechend zurückgezahlt werden

• Wenn der Schuldner seine Zahlungsverpflichtungen gegenüber dem Gläubiger jeweils zum Jahresende in gleich bleibenden Beträgen leistet, heißen diese (Schuld-)Annuitäten.

Annuitätendarlehen

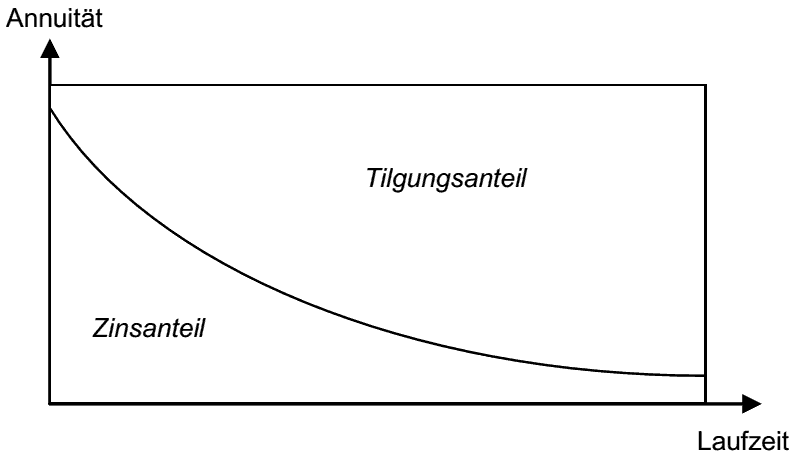
• Annuitätenrechnung aus Investorensicht

• bei der Durchführung einer Investition sind die beteiligten Investoren oft nicht an Einmalzahlungen interessiert, d. h. der Entnahme des positiven Bar- oder Endwertes, sondern an jährlichen Zahlungen über die gesamte Laufzeit

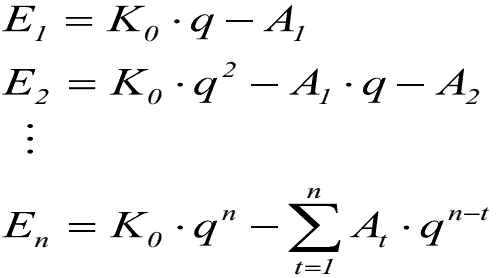
• da am Ende der Laufzeit der Endwert E_n = 0 ist, ergibt sich für die Annuität:

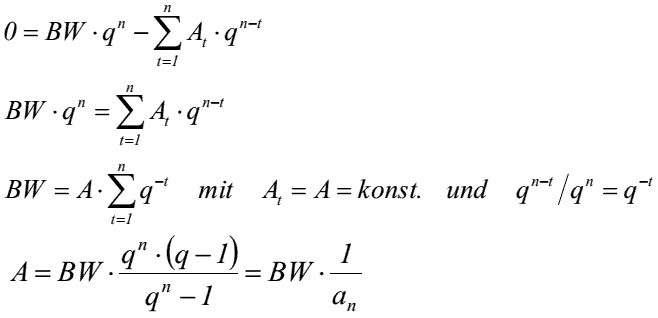
• Äquivalente jährliche Zahlungen in konstanter oder wachsender Höhe - die neben Zins und Tilgung in jeder Periode zur Verfügung stehen - heißen Gewinnannuitäten oder nur Annuitäten.

---

CategoryBwl2⇒