Version [91367]
Dies ist eine alte Version von TutoriumDokumentstrukturanalyseSS18 erstellt von MoD am 2018-09-26 01:09:09.
Tutorium: Dokumentstrukturanalyse
1. Tutoren:
Jordan Zapf
2. Ziel des Tutoriums:
- Aufbau von Grundverständnis für Distanzmaße
- Vergleich von verschiedenen Ähnlichkeitskoeffizienten
- Programmierung der Levenshtein-Distanz
3. Adressaten des Lehrangebotes:
Interessierte Studenten der Fakultät Informatik
4. Teilnahme:
Wird durch Rundmail bekannt gegeben.
5. Veranstaltungsinhalte:
Distanzmaße
Ähnlichkeitsmaße/ Distanzmaße werden im Rahmen der Datenanalyse (z.B. Clusteranalyse; Multidimensionale Skalierung) zur Bestimmung der Beziehungen zwischen Messobjekten eingesetzt. Dabei werden durch Vergleiche von metrisch skalierten Ausgangsdaten (Skalenniveau) die zwischen Objekten bestehenden Ähnlichkeiten gemessen. Ist die Distanz gering, dann ist die Ähnlichkeit groß; entsprechend sind sich Objekte bei großer Distanz sehr unähnlich.
Clusteranalyse
Oberbegriff für einen Typ der in der multivariaten Analyse und vor allem in der Clusteranalyse verwendeten Proximitätsmaße, mit denen im Gegensatz zu den Ähnlichkeitsmaßen und den - Korrelationsmaßen die Entfernungsbeziehung zwischen Meßobjekten bestimmt wird. Durch sie wird die Entfernung zwischen Objekten im n-dimensionalen - Merkmalsraum bestimmt. Voraussetzung für die Verwendung von Distanzmaßen ist das Vorliegen intervallskalierter Daten. Die Anwendung von Distanzmaßen ist neben der Clusteranalyse auch in vielen anderen Bereichen der Datenanalyse sinnvoll, so bei Skalierungsverfahren und hier insbesondere bei multidimensionalen Skalierungsverfahren und bei der Diskriminanzanalyse (z.B. Mahalanobis-Distanz).
Die beiden am meisten verwendeten Distanzmaße sind Sonderfälle der zur größeren Familie der als Minkowski-Metrik bezeichneten zählenden Distanzmaße in der allgemeinen Form:

Dabei bezeichnet d die Distanz zwischen den Punkten j und k bei Beachtung des Minkowski-Parameters r; xja und xka sind die Koordinatenwerte des Objekts j(k) auf den Achsen a(a = 1,2, ... , m) und r ist der Metrik-Parameter (1 > r > 0). Daraus lassen sich die beiden am meisten verwendeten Distanzmaße, die Euklidische Distanz und die City-Block Distanz ableiten.
City-Block-Distanz(Manhattan)
Setzt man in die Minkowski-Metrik für r = 1 ein, ergibt sich die City-Block-Distanz:

Die Bezeichnung City-Block-Distanz ist aus dem Bild rechteckig angelegter Straßenzüge abgeleitet, in denen die Entfernung von einem Punkt zum anderen nicht durch die in Form der Luftlinie angegebene kürzeste Distanz zwischen zwei Punkten, sondern nur durch Entlangfahren an den Straßenzügen zurückgelegt werden kann. Im angelsächsischen Sprachraum spricht man deshalb auch von der Manhattan-Distanz bzw. der Taxifahrer-Distanz (taxicab metric).
Euklidische Distanz
Setzt man in die Minkowski-Metrik für r = 2 ein, ergibt sich die Euklid-Distanz:

wobei xja und xka die Projektionen der Punkte j und k auf die Dimension a(a = 1,2, ..., m) darstellen. Durch die Euklidische Distanz wird die kürzeste Distanz zwischen zwei Objekten angegeben.
Euklidische u. City-Block-Distanz im Vergleich

Ähnlichkeitskoeffizienten
Ähnlichkeitskoeffizienten im Vergleich

Einteilung der Objekte

Einfaches Beispiel
Rohdaten
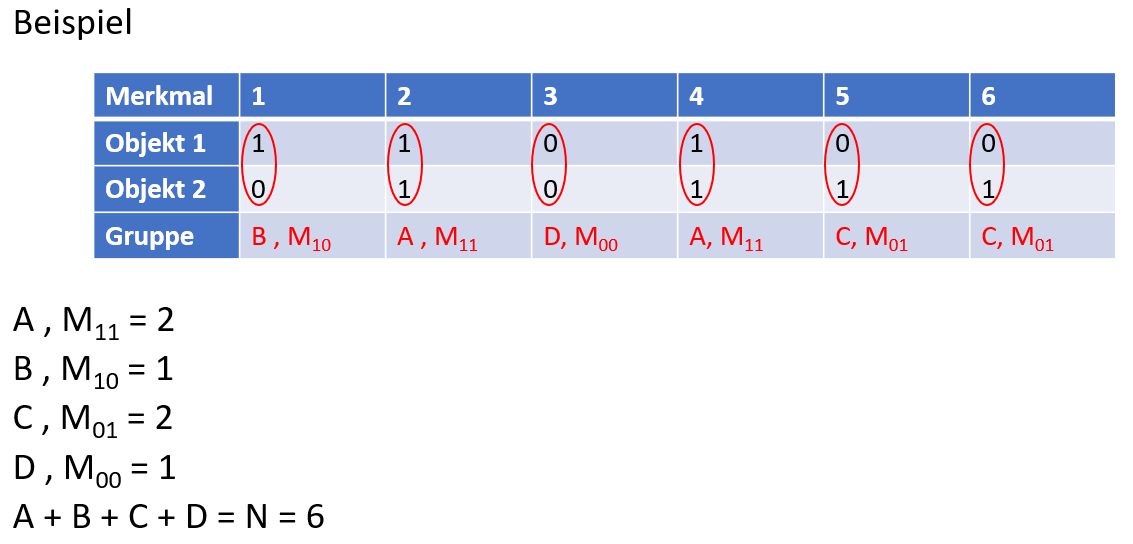
Berechnung

Großes Beispiel
Rohdaten

Ergebnis Tanimoto/Jaccard

Levenshtein-Distanz
| File | Last modified | Size |
|---|---|---|
| ak1.png | 2023-10-06 18:37 | 36Kb |
| ak2.png | 2023-10-06 18:37 | 52Kb |
| ak3.png | 2023-10-06 18:37 | 30Kb |
| ak3_2.png | 2023-10-06 18:37 | 28Kb |
| ak4.png | 2023-10-06 18:37 | 41Kb |
| ak5.png | 2023-10-06 18:37 | 60Kb |
| ak6.png | 2023-10-06 18:37 | 67Kb |
| cluster.png | 2023-10-06 18:37 | 5Kb |
| euklidisch.png | 2023-10-06 18:37 | 4Kb |
| ld1.png | 2023-10-06 18:37 | 29Kb |
| ld2.png | 2023-10-06 18:37 | 24Kb |
| ld3.png | 2023-10-06 18:37 | 34Kb |
| ld4.png | 2023-10-06 18:37 | 29Kb |
| ld5.png | 2023-10-06 18:37 | 120Kb |
| manhattan.png | 2023-10-06 18:37 | 7Kb |
| manhattan2.png | 2023-10-06 18:37 | 3Kb |

