Tutorium Mathematik 3
Variation der Konstanten
| Vorgehensweise |
|---|
Diese Methode bietet sich für lineare inhomogene DGL mit konstanten Koeffizienten an, wenn die Störfunktion nicht auf einen einfachen Ansatz für eine partikuläre Lösung hinweist. Darüber hinaus ist die Methode auch oft für lineare homogene DGL mit konstanten Koeffizienten geeignet. Im einfachsten Fall einer inhomogenen DGL erster Ordnung wird wie folgt vorgegangen: Die freie Konstante der allgemeinen Lösung C der zugehörigen homogenen DGL wird als Funktion C (x) von x betrachtet. Durch Einsetzen in die inhomogene DGL erhält man eine einfachere DGL für C (x), welches dann bestimmt werden kann. Beispiel: Anfangsbedingung: y(-5) = -8 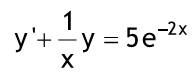 y'+(1/x)y=5e^(-2x) zug. hom. DGL: 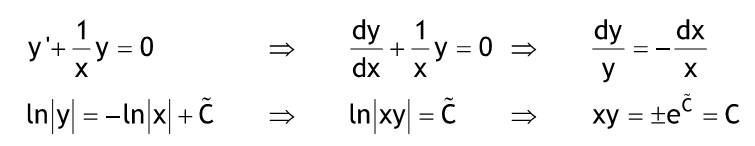 y'+(1/x)y=0->(dy)/(dx)+(1/x)y=0->(dy)/y=-(dx)/x ln Betrag von y = -ln Betrag von x + Cgestrichen -> ln Betrag von xy = Cgestrichen -> xy = +-e^C gestrichen = C homogene Lösung: yH = C/X Ansatz:  y=C(x)/x -> y' = -C(x)/x^2 + C'(x)/x einsetzen: 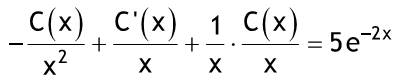 -C(x)/x^2 + C'(x)/x + 1/x* C(x)/x = 5e^(-2x) einfache DGL für C(x) 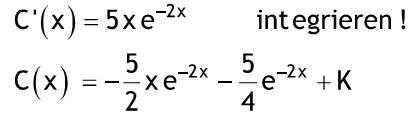 C'(x)=5xe^(-2x) integrieren ! C(x)=-5/2xe^(-2x)-5/4e^(-2x)+k in Ansatz einsetzen: 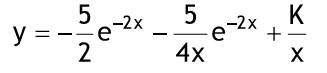 = allgemeine Lösung = allgemeine Lösungy=-5/2e^(-2x)-5/(4x)e^(-2x)+k/x=allgemeine Lösung Anfangsbedingung: 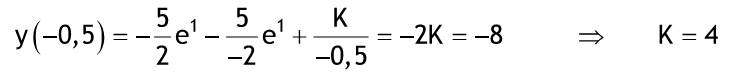 y(-0,5)=-5/2e^1-5/-2e^1+k/-0,5=-2k=-8 -> k=4 spezielle Lösung: 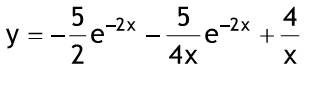 y=-5/2e^(-2x)-5/(4x)e^(-2x)+4/x |
| PDF Dokument Variation der Konstanten |

