Version [73398]
Dies ist eine alte Version von TutoriumMathe3L9 erstellt von Jorina Lossau am 2016-10-24 17:04:36.
Tutorium Mathematik 3
Laplace - Transformation - Lösungen
| Aufgabe 2.1 Nachfolgend für t ≥ 0 definierte Funktionen haben für t < 0 den Funktionswert f(t) = 0. Transformieren Sie mit der Tabelle in den Bildbereich der Laplace-Transformation! 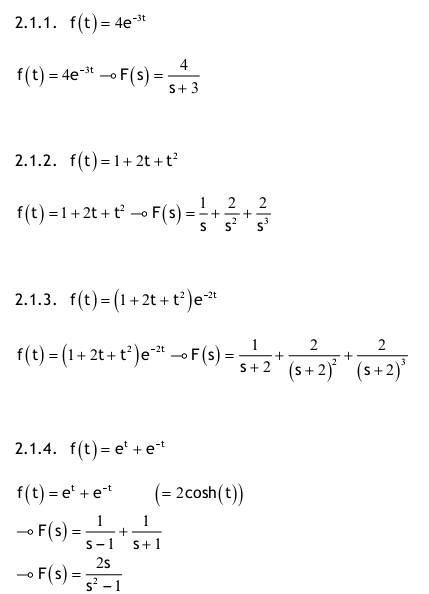 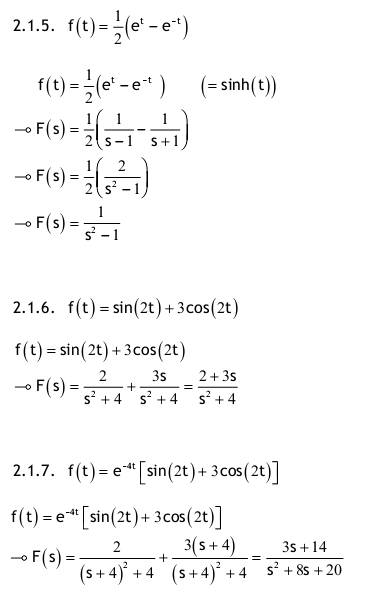 2.1.1. f(t)=4e^(-3t) ->F(s)=4/(s+3) 2.1.2. f(t)=1+2t+t^2 ->F(s)=1/s+2/s^2+2/s^3 2.1.3. f(t)=(1+2t+t^2)e^(-2t) ->F(s)=1/(s+2)+2/(s+2)^2+2/(s+2)^3 2.1.4. f(t)=e^t+e^(-t) ->F(s)=1/(s-1)+1/(s+1) ->F(s)=2s/(s^2-1) 2.1.5. f(t)=1/2(e^t-e^(-t)) (=sinh(t)) ->F(s)=1/2((1/(s-1)-1/(s+1)) ->F(s)=1/2((2/(s^2-1)) ->F(s)=1/(s^2-1) 2.1.6. f(t)=sin(2t)+3cos(2t) ->F(s)=2/(s^2+4)+3s/(s^2+4)=(2+3s)/(s^2+4) 2.1.7. f(t)=e^(-4t)[sin(2t)+3cos(2t)] ->F(s)=(2/(s+4^2+4))+(3(s+4)/((s+4)^2+4))=(3s+14)/(s^2+8s+20) Aufgabe 2.2 Berechnen Sie die Bildfunktion unter Verwendung des Integrals, welches die Laplace-Transformation definiert. 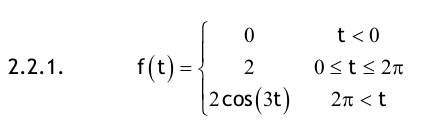 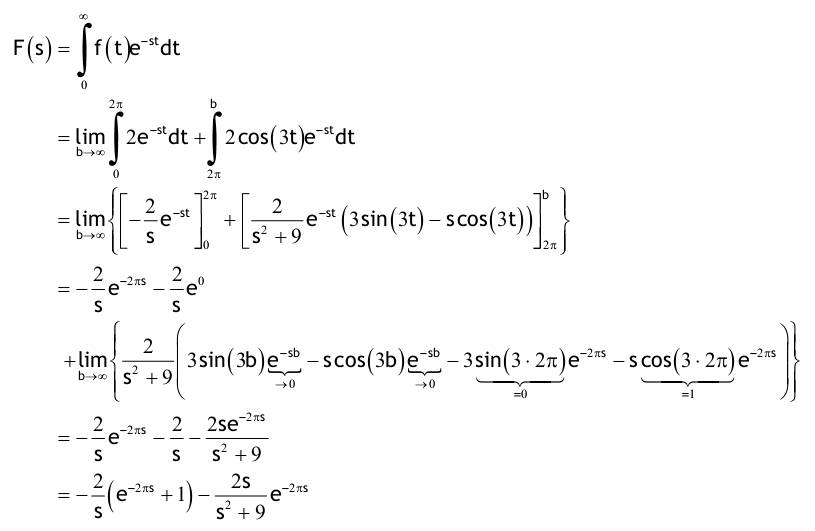  2.2.1. f(t)= (0; t<0) (2; 0<t<2π) (2cos(3t), 2π<t) 2.2.2. f(t)= (0, t<0) (A, 0<t<3) (Ae^(-t-3), 3<t) Aufgabe 2.3 Transformieren Sie mit der Tabelle der Laplace-Korrespondenzen vom Bild- in den Zeitbereich. Falls nötig, zerlegen Sie die Ausdrücke zunächst in Partialbrüche.  Zählervergleich: 2 = A(s-2) + B(s+2) 1. Weg: Nullstellen einsetzen: s = 2--> 2 = 4B s = -2-->2 = -4A   Zählervergleich: s = A(s-2) + B(s+2) 1. Weg: Nullstellen einsetzen s = 2 -->2 = 4B s = -2 -->-2 = -4B   1. Weg: Partialbruchzerlegung:  Zählervergleich:  2. Weg: Differentationsregel    1. Weg: Partialbruchzerlegung:  Zählervergleich:  2. Weg: Differentationsregel:   1. Weg: Partialbruchzerlegung:  Zählervergleich:  2. Weg: Differentationsregel:   Der Nenner hat konjugiert komplexe Nullstellen. Deshalb ist quadratische Ergänzung zweckmäßiger als Partialbruchzerlegung.   Wie in 3.12 wird auch hier die quadratische Ergänzung benutzt   Wie in 3.12 wird auch hier die quadratische Ergänzung benutzt  Aufgabe 2.4 Führen Sie die Partialbruchzerlegung durch und transformieren Sie danach in den Zeitbereich.  Zählervergleich: 1 = A (s+1) + Bs    Nullstellen einsetzen: s = -1 --> -1 = A s = -2 --> -2 = -C Koeffizienten - Vergleich:   Zählervergleich: s = A(s²+2) + (Bs+C)(s+1) Nullstellen einsetzen: s = -1 --> -1 = 3A   Nullstellen einsetzen: s = 1--> 5 = 34A Koeffizienten - Vergleich:  Aufgabe 2.5 Lösen Sie folgende Anfangswertaufgaben mit der Laplace-Transformation.  Nullstellen einsetzen:    Zählervergleich: 3 = A(s+1)(s-5) + B(s-2)(s-5)+C(s-2)(s+1) Nullstellen einsetzen:   Nullstellen einsetzen: s = 5 --> 3 = 204D s = -1 --> 3 = -60C Koeffizienten - Vergleich:   Nullstellen einsetzen: s = 5 --> 5 = 246D s = -1 --> -1 = -102C Koeffizienten - Vergleich:   Zählervergleich: 7 = As(s-5)+Bs(s+1)+C(s+1)(s-5) Nullstellen einsetzen:   Nullstellen einsetzen: s = 5 --> 2 = 750B s = -1 --> 2 = 6A s = 0 --> 2 = -5E Koeffizienten - Vergleich:   Koeffizienten - Vergleich:   Nullstellen einsetzen: s = -3 --> 32 = -18B s = -1 --> 4 = 2A s = 0 --> 2 = 3D Achtung !!! Die zweite Anfangsbedingung y(0) = 0 wird nicht erfüllt. Überzeugen Sie sich davon, indem Sie die erste Ableitung von y bilden und t = 0 einsetzen. Für die spezielle Lösung einer DGL 1. Ordnung ist i.a. nur eine Zusatzbedingung notwendig. Weitere Bedingungen könnten dann nur rein zufällig auch erfüllt sein, was aber hier nicht zutrifft.   Achtung !!! Wie in 2.5.9 ist die Anfangsbedingung y(0) = 0 nicht erfüllt !  Zählervergleich:  Aufgabe 2.6 Transformieren Sie in den Zeitbereich unter Verwendung der Faltungsregel!   |
| PDF Dokument Lösungen Laplace - Transformation |

