Tutorium Elektrotechnik 3
Resonanzerscheinungen - Lösung
| 1.1 Aufgabe 1 Gegeben ist ein Parallelschwingkreis mit R = 8Ω, C = 0,2H und C = 120nF. An diesem Schwingkreis wird eine Spannungsquelle mit U = 230V und f = 50Hz angeschlossen. a) Geben Sie die Scheinimpedanz sowie die Scheinadmitanz an. b) Berechnen Sie IR, IL und IC und fertigen sie (qualitativ) ein Zeigerdiagramm der Ströme an. c) Berechnen Sie die Resonanzfrequenz wr bzw. fr. d) Berechnen Sie die Güte und den Verlustfaktor des Schwingkreises. e) Berechnen Sie die obere und untere Grenzfrequenz sowie die Bandbreite. f) Zeichnen Sie die Widerstands- und Leitwertortskurve. g) Wo liegt in der Ortskurve die Resonanzfrequenz? Lösung: a) Y=1/R+j(wC)-1/(wL) Z=(1/R)/((1/R)^2+(wC-1/(wL))-j((wC-1/(wL))/(R^2+(wC-1/(wL)^)2) b) IR=28,75A IL=3,657A*e^(-j90Grad) IL=8,670mA*e^(j90Grad) c) fr=1025,34Hz wr=6454,97s^-1 d) Q=6,197*10^-3 ds=161,37 e) B=165780,22Hz w1=40Hz w2=1,042MHz 1.2 Aufgabe 2 Gegeben ist folgende Schaltung: 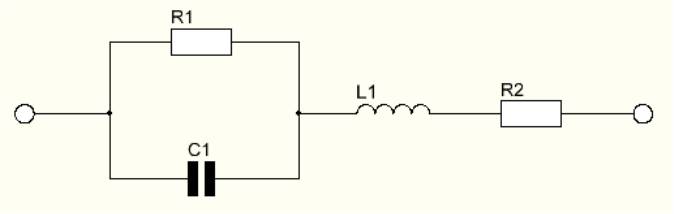 mit R1 = 10Ω, R2 = 100Ω, C = 70nF und L = 400mH. a) Geben Sie die Impedanz der Schaltung an. b) Berechnen Sie die Resonanzfrequenz wr. c) Berechnen Sie die Güte und die Dämpfung.(Hinweis: Umwandlung der Parallelschaltung in eine äquivalente Reihenschaltung) Lösung: a) Z=R2+(1/R1)/((1/R1)^2(wC1)^2)+j(wC1-(wC1/(1/R1)^2+(wC1)^2)) b) wr=5855,4s^-1 c) Rr=100Ω Cr=7qF Q=0,4687 d=2,139 |
| PDF Dokument Lösungen |

