Tutorium Mathematischer Grundkurs
Umformen und Vereinfachen Mathematischer Terme - Lösungen
| Berechnen Sie ohne Taschenrechner (erst möglichst viel kürzen, Primfaktorzerlegung!) 0.1.1.T A = 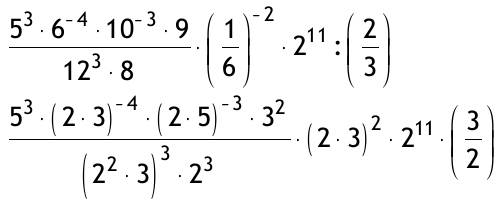 A =(5^3*3^2*2^2*3^2*2^11*3)/(2^4*3^4*2^3*5^3*2^6*3^3*2^3*2) A =1/(2^4*3^2) = 1/(4*3)^2 =1/144 0.1.2.T B = 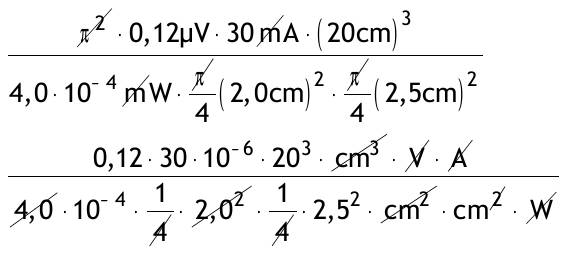 = (0,12*30*10^-6*8*10^3)/(10^-4*5^2*2^-2) = (12*3*8*4)/5^2 = ((3*2^2*3*2^3*2^2)/5^2)* (2^2/2^2) = (2^9*9)/100 = 5,12*9 = 46,08 1/cm Fassen Sie auf einen gemeinsamen Nenner zusammen, beseitigen Sie ggf. Mehrfachbrüche und machen Sie ggf. den Nenner rational 0.1.3.T a) Rp = 1/(1/R1 + 1/R2) (1/Rp)* (R1R2/R1R2) = (1/R1)*(RpR2/RpR2)+1/R2*(RpR2/RpR2) R1R2/RpR1R2 = RpR2/RpR1R2 + RpR1/RpR1R2 R1R2 = RpR2 + RpR1 umstellen nach R1: R1R2 - RpR1 = RpR2 R1(R2-Rp) = RpR2 R1 = (Rp*R2)/(R2-Rp) b) Rp = 1/(1/R1 + 1/R2 + 1/R3) 1/Rp = 1/R1 + 1/R2 + 1/R3 1/R1 = 1/Rp - 1/R2 - 1/R3 = (R2R3 - RpR3 - RpR2) / RpR2R3 R1 = (RpR2R3)/ R2R3 - RpR3 - RpR2 0.1.4.T a) 1/xy + 1/xz + 1/yz = z/xyz + y/xyz + x/xyz = (x+y+z)* 1/xyz b) (u/v - v/u)*(u/v+v/u) = (u²+v²/uv) = (1/(uv)²)* (u²-v²)* (u²+v²) = (1/(uv)²)* (u^4-v^4) c) (x+y/x-y) + (x-y/ x+y) = ((x+y)² + (x-y)²)/((x-y)*(x+y)) = (x² + 2xy + y² + x² - 2xy + y²)/x²-y² = (2x² + 2y²)/ (x²-y²) d) (x²/y + y²/x)/(1/x + 1/y) = 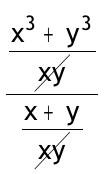 = x³+y³/x+y e) √27/(√6-√3) = √(3*9)/(√(2*3)-√3) = 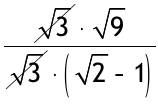 = (3/(√2-1))* (√2+1/√2+1) = (3*√2+3)/(2-1) =3*√2+3 |
| PDF Dokument Lösungen Mathematische Terme |

