Das Fehlerrückkopplungsnetz
Das Fehlerrückkopplungsnetz (= error backpropagation) ist ein überwachtes Lernverfahren.
Das bedeutet, dass es einen Experten geben muss der zu jedem Eingabemuster die Ausgabe kennt.
Das Netz besteht aus mindestens 2 Schichten die vollständig vernetzt sind.
Das Netz lernt durch ändern der (Kanten-) Gewichte (zwischen den einzelnen Schichten).
A. Aufbau
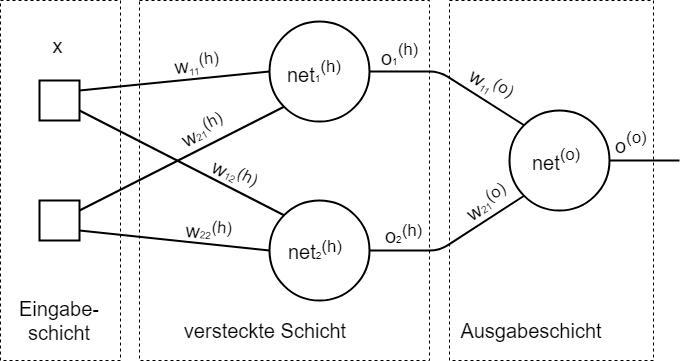
Lernregel Ausgabeschicht:
formel
\Delta \omega_{ij}^{(o)} = \eta o_i^{(h)} * \delta_j^{(o)T}formel
formel
\etaformel
- Lernschrittweiteformel
\delta_j^{(o)T}formel
- Aktivierungsfehler beim empfangenden Neuronformel
o_i^{(h)}formel
- Ausgabe des sendendes Neuronsformel
\delta_j^{(o)}formel
Lernregel versteckte Schicht:
formel
\Delta \omega_{ij}^{(h)} = \eta x_i \delta_j^{(h)T}formel
formel
\etaformel
- Lernschrittweiteformel
\delta_j^{(h)T}formel
- Aktivierungsfehler beim empfangenden Neuronformel
x_iformel
-Eingabe (Trainingsmuster)Zielfunktion: minimiere den mittleren quadratischen Fehler der Ausgabeschicht
formel
E= (\frac 12) \sum_{j=1}^{n_N^{(o)}} \delta_j^{(o)^2}formel
Dieser Fehler muss immer positiv seinB. Vorgehensweise:
gegeben sein ein neuronales Netz, eine Eingabe (Trainingsmuster), Ausgabe (des Trainingsmusters vom Experten, diese wird erst bei der Berechnung des Fehlers benötigt)
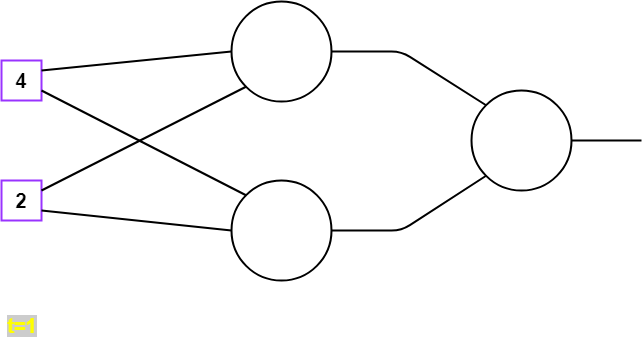
formel
x= \left\lgroup \matrix{4 \cr 2}\right\rgroupformel
t=11. Gewichte werden (zufällig) initialisiert
formel
\omega^{(h)} = \left\lgroup \matrix{0.11 & 0.17\cr 0.15 & 0.13}\right\rgroupformel
formel
\omega^{(o)} = \left\lgroup \matrix{0.2 \cr 0.25}\right\rgroupformel
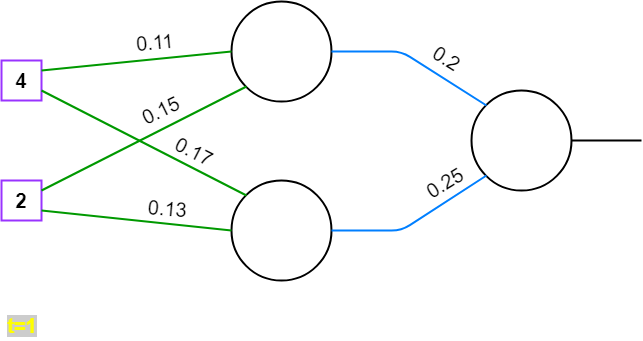
2. Vorwärtsrechnen
Regeln:
formel
net^{(h)}= \omega^{(h)T} xformel
formel
net^{(o)}= \omega^{(o)T} o^{(o)}formel
formel
o^{(h)}= f'_{act}(net^{(h)})formel
formel
o^{(o)}= f'_{act}(net^{(o)})formel
Anwenden:
formel
net^{(h)}= \omega^{(h)T} xformel
formel
net^{(h)}= \left\lgroup \matrix{0.11 & 0.17\cr 0.15 & 0.13}\right\rgroup ^T \left\lgroup \matrix{4 \cr 2}\right\rgroupformel
formel
net^{(h)}= \left\lgroup \matrix{0.11 & 0.15\cr 0.17 & 0.13} \right\rgroup \left\lgroup \matrix{4 \cr 2}\right\rgroupformel
formel
net^{(h)}=\left\lgroup \matrix{0.74 \cr 0.94}\right\rgroupformel
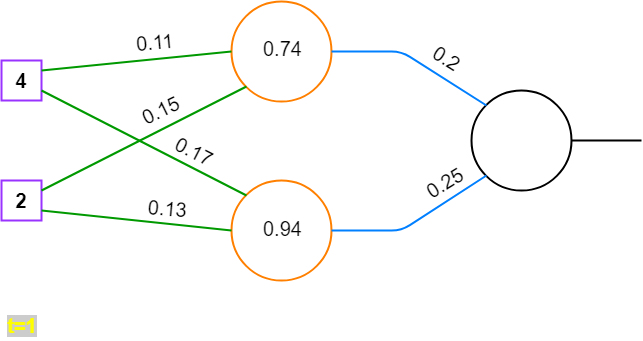
formel
o^{(h)}=f'_{act}(net^{(h)}formel
formel
f'_{act}(net^{(h)}formel
, ist die Aktivierungsfunktion des Neurons. In der Praxis bestimmt sie, ob ein Neuron sich aktiviert (feuert) oder nicht. Sie muss differenzierbar sein, also ihre Ableitung darf nicht überall gleich null sein.In diesem Beispiel soll sie aber keine große Rolle spielen. Zur Vereinfachung, wir die Vereinbarung getroffen, dass die Neuronen immer feuern.
Dadurch ergibt sich:
formel
o^{(h)}=net^{(h)}formel
Das gilt analog für die Ausgabeschicht:
formel
net^{(o)} = \omega^{(o)T} o^{(h)}formel
formel
net^{(o)} = \left\lgroup \matrix{0.2 \cr 0.25}\right\rgroup ^T \left\lgroup \matrix{0.74 \cr 0.94} \right\rgroupformel
formel
net^{(o)}= \left\lgroup \matrix{0.2 & 0.25}\right\rgroup \left\lgroup \matrix{0.74 \cr 0.94} \right\rgroupformel
formel
net^{(o)} = (0.383)formel
formel
o^{(o)}=net^{(o)}formel
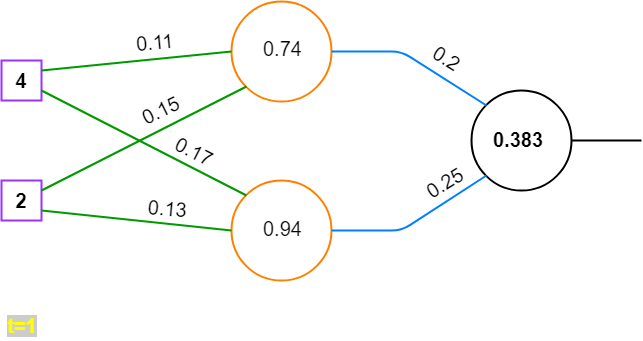
3. Fehler berechnen
formel
E= (\frac 12) \sum_{j=1}^{n_N^{(o)}} \delta_j^{(o)^2}formel
, ist der Gesamtfehler aller Ausgänge. Bei größeren Netzen, würden mehrere Ausgabewerte entstehen, die alle mit der erwarteten Ausgabe des Experten verglichen werden müssen. Der absolute Fehler jedes Ausgabe-Neurons ist dabeiformel
\delta_j^{(o)} = o_j^{(o)}-t_jformel
.Anwendung:
In diesem Beispiel gibt es nur einen Ausgabewert.
Daher ist
formel
\delta^{(o)} = o^{(o)}-tformel
formel
\delta^{(o)} = (0.383) - 1 = -0.617formel
formel
E=(\frac 12)*(-0.617)^2 = 0.19formel
E soll minimiert werden.
formel
\delta^{(o)}formel
soll 0 sein. In der Praxis wirdformel
\delta^{(o)}formel
nur sehr selten wirklich 0 werden, er sollte aber so nah wie möglich an 0 sein.4. Lernschrittweite
Die Lernschrittweite ist ein Faktor der angibt, wie stark das neuronale Netz in jedem Schritt adaptiert wird. Sie wird meistens vom Anwender des neuronalen Netzes festgelegt. Es gibt auch Varianten, wo die Lernschrittweite dynamisch oder fortlaufend (periodisch) angepasst wird.
In diesem Beispiel soll
formel
\eta=0.1formel
sein und sich nicht verändern.5. Fehler zurückführen
Regel:
formel
\Delta \omega_{ij}^{(o)} = \eta o_i^{(h)} \delta_j^{(o)T}formel
formel
'\omega^{(o)} = \omega^{(o)} - \Delta \omega_{ij}^{(o)}formel
formel
'\omega^{(o)} = \omega^{(o)} - \eta o_i^{(h)} \delta_j^{(o)T}formel
formel
\Delta \omega_{ij}^{(h)} = \eta x_i \delta_j^{(h)}formel
formel
'\omega^{(h)} = \omega^{(h)} - \Delta \omega_{ij}^{(h)}formel
formel
'\omega^{(h)} = \omega^{(h)} - \eta x_i \delta_j^{(h)T}formel
formel
\delta_j^{(h)} = \sum_{i=1} \omega_{ij}^{(o)} \delta_i^{(o)}formel
formel
'\omega - neues Kantengewichtformel
Anwendung:
formel
'\omega^{(o)} = \omega^{(o)} - \eta o_i^{(h)} \delta_j^{(o)T}formel
formel
'\omega^{(o)} = \left\lgroup \matrix{0.2 \cr 0.25}\right\rgroup -0.1 * \left\lgroup \matrix{0.74 \cr 0.94}\right\rgroup * (-0.617)formel
formel
'\omega^{(o)} = \left\lgroup \matrix{0.2457 \cr 0.308}\right\rgroupformel
formel
'\omega^{(h)} = \omega^{(h)} - \eta x_i \delta_j^{(h)T}formel
formel
'\omega^{(h)} = \left\lgroup \matrix{0.11 & 0.17 \cr 0.15 & 0.13}\right\rgroup - 0.1 * \left\lgroup \matrix{4 \cr 2}\right\rgroup * \left\lgroup \matrix{0.2*(-0.617) \cr 0.25*(-0.617)}\right\rgroup^Tformel
formel
'\omega^{(h)} = \left\lgroup \matrix{0.1594 & 0.2317 \cr 0.1747 & 0.1608}\right\rgroupformel
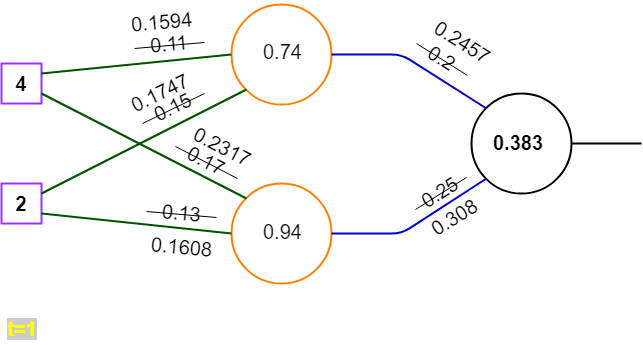
6. erneut Vorwärtsrechnen mit aktualisierten Gewichten
Wir erinnern uns:
Regel:
formel
net^{(h)}= \omega^{(h)T} xformel
formel
net^{(o)}= \omega^{(o)T} o^{(o)}formel
formel
o^{(h)}= f'_{act}(net^{(h)})formel
formel
o^{(o)}= f'_{act}(net^{(o)})formel
Anwenden:
formel
net^{(h)}= \omega^{(h)T} xformel
formel
net^{(h)}= \left\lgroup \matrix{0.1594 & 0.2317 \cr 0.1747 & 0.1608}\right\rgroup^T \left\lgroup\matrix{4 \cr 2}\right\rgroupformel
formel
net^{(h)}= \left\lgroup \matrix{0.1594 & 0.1747 \cr 0.2317 & 0.1608}\right\rgroup \left\lgroup\matrix{4 \cr 2}\right\rgroupformel
formel
net^{(h)} = \left\lgroup \matrix{0.9868 \cr 1.2485}\right\rgroupformel
Wir erinnern uns:formel
o^{(h)}=net^{(h)}formel
formel
net^{(o)} = \omega^{(o)T} o^{(h)}=formel
formel
net^{(o)} = \left\lgroup \matrix{0.2457 \cr 0.308}\right\rgroup ^T \left\lgroup \matrix{0.9868 \cr 1.2485}\right\rgroupformel
formel
net^{(o)} = \left\lgroup \matrix{0.2457 & 0.308}\right\rgroup \left\lgroup \matrix{0.9868 \cr 1.2485}\right\rgroupformel
formel
net^{(o)} = \left\lgroup \matrix{0.6270}\right\rgroupformel
Wir erinnern uns:formel
o^{(o)}=net^{(o)}formel
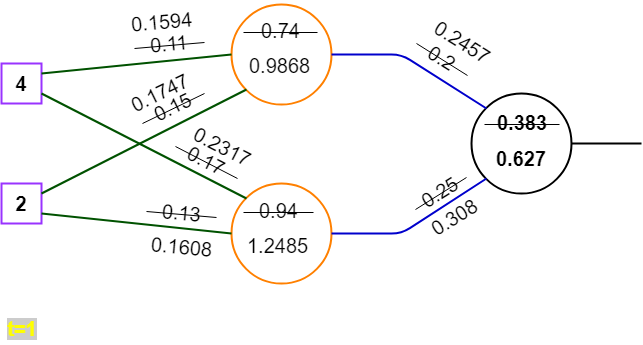
7. aktuellen Fehler berechnen
Wir erinnern uns:
formel
E= (\frac 12) \sum_{j=1}^{n_N^{(o)}} \delta_j^{(o)^2}formel
formel
\delta^{(o)} = o^{(o)}-tformel
formel
\delta^{(o)}=(0.627) - 1 = -0.373formel
formel
E= (\frac 12) * (-0.373)^2 = 0.06956formel
0.627 ist näher an 1 dran, als 0.383.
Der Fehler ist kleiner geworden, das Netz ist jetzt besser adaptiert.
In der Praxis würde dieser Fehler jetzt wieder zurück gerechnet werden und anschließend wieder vorwärts usw. solange bis, er Null ist oder ein Abbruchkriterium erfüllt ist.
Diese Abbruchkriterien könnten sein, dass der Fehler nah genug an Null ist (Schwellwert) oder dass eine (vorher eingestellte) maximale Anzahl an Durchläufen durchgerechnet worden sind.
Quellen:
https://medium.com/datathings/neural-networks-and-backpropagation-explained-in-a-simple-way-f540a3611f5e
https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/

